题目内容
在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于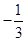 .
.
(1)求动点P的轨迹方程;
(2)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由.
【答案】
(1)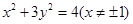 ;(2)存在,且点
;(2)存在,且点 的坐标为
的坐标为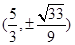 .
.
【解析】
试题分析:(1)本题只要直接设出动点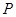 的坐标为
的坐标为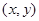 ,用
,用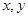 表示出已知条件
表示出已知条件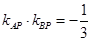 ,即可求出所求轨迹方程;(2)此问题存在性问题,解决的方法是假设这个点存在,然后根据已知条件去求这个点,若能求出,则存在,若求不出,则不存在在.即设存在题设的
,即可求出所求轨迹方程;(2)此问题存在性问题,解决的方法是假设这个点存在,然后根据已知条件去求这个点,若能求出,则存在,若求不出,则不存在在.即设存在题设的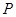 点,其坐标为
点,其坐标为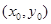 ,然后求出
,然后求出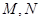 的坐标,进而求出
的坐标,进而求出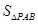 和
和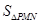 ,令
,令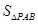 =
=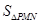 ,求
,求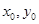 .当然考虑到△PAB与△PMN有一对对顶角,也可这样求三角形的面积:
.当然考虑到△PAB与△PMN有一对对顶角,也可这样求三角形的面积: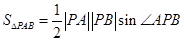 ,
,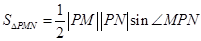 ,由于
,由于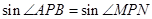 ,所以由
,所以由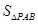 =
=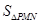 ,得
,得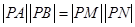 ,也即
,也即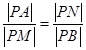 ,这个式子可很快求出
,这个式子可很快求出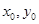 .
.
试题解析:(1)解:因为点B与A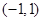 关于原点
关于原点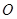 对称,所以点
对称,所以点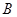 得坐标为
得坐标为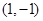 ,
,
设点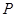 的坐标为
的坐标为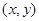 由题意得
由题意得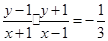 ,化简得:
,化简得: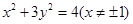 .
.
故动点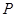 的轨迹方程为:
的轨迹方程为: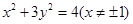 4分
4分
(2)解法一:设点P的坐标为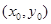 ,点M,N的坐标为
,点M,N的坐标为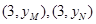 ,
,
则直线AP的方程为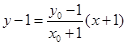 ,直线BP的方程为
,直线BP的方程为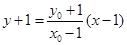 ,
,
令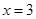 ,得
,得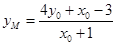 ,
,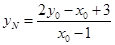 .
.
于是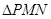 的面积是
的面积是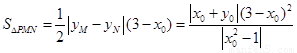 ,
,
又直线AB的方程为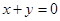 ,
,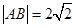 ,点P到直线AB的距离
,点P到直线AB的距离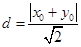 ,
,
于是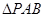 的面积
的面积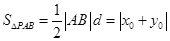
当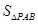 =
=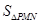 时,
时,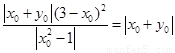 ,
,
又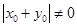 ,∴
,∴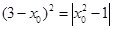 ,解得
,解得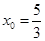 ,
,
又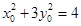 ,∴
,∴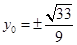 ,
,
故存在点P使得△PAB与△PMN的面积相等,此时P点坐标为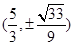 .
.
解法二:若存在点 使得
使得 与
与 的面积相等,设点
的面积相等,设点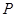 的坐标为
的坐标为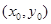
则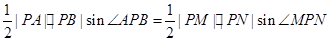 .
.
因为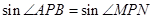 , 所以
, 所以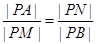 ,
,
所以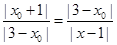 即
即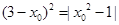 ,解得
,解得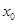
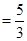 .
.
因为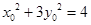 ,所以
,所以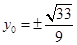 故存在点
故存在点 S使得
S使得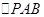 与
与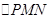 的面积相等,此时点
的面积相等,此时点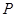 的坐标为
的坐标为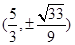 .
10分
.
10分
考点:(1)直接法求轨迹方程;(2)解析几何综合问题.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是