题目内容
下列命题中正确的是 ( )
A. 的最小值是2 的最小值是2 | B. 的最小值是2 的最小值是2 |
C. 的最小值是 的最小值是 | D. 的最大值是 的最大值是 |
C
解析试题分析: 选项A中,由于 只有x>0时,函数取得最小值2,故不成立。选项B中,由于
只有x>0时,函数取得最小值2,故不成立。选项B中,由于 ,等号不成立,那么不能得到最小值为2,故错误。选项C中,由于
,等号不成立,那么不能得到最小值为2,故错误。选项C中,由于 ,只有利用函数的单调性可知当x=2,或者x=
,只有利用函数的单调性可知当x=2,或者x=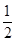 时,结合均值不等式得到最值。选项D中,由于
时,结合均值不等式得到最值。选项D中,由于 的最大值是
的最大值是 ,成立的前提是x>0,故选C.
,成立的前提是x>0,故选C.
考点:本题主要考查了均值不等式的求解的运用。
点评:解决该试题的关键是能力用均值不等式的一正二定三相等的思想来分析最值是否取得,进而分析得到。

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
若 ,函数
,函数 在
在 处有极值,则
处有极值,则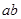 的最大值是( )
的最大值是( )
| A.9 | B.6 | C.3 | D.2 |
已知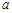 ,
,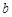 为实数,且
为实数,且 ,则下列命题错误的是
,则下列命题错误的是
A.若 , , ,则 ,则 | B.若 ,则 ,则 , , |
C.若 ,则 ,则 | D.若 ,则 ,则 |
设 是实数,且满足等式
是实数,且满足等式 ,则实数
,则实数 等于( )(以下各式中
等于( )(以下各式中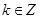 )
)
A.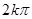 | B. | C. | D. |
已知 ,则
,则 的最小值是( )
的最小值是( )
| A.3 | B.4 | C. | D. |
.已知实数 ,则M的最小值为( )
,则M的最小值为( )
A. | B.2 | C.4 | D.1 |
已知x,y 都是正数,若  , 则
, 则 有( )
有( )
| A.最小值16 | B.最大值16 | C.最小值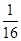 | D.最大值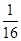 |
已知 ,函数
,函数 的最小值是 ( )
的最小值是 ( )
| A.5 | B.4 | C.8 | D.6 |
 ≥a恒成立,则实数a的最大值为_____________.
≥a恒成立,则实数a的最大值为_____________.