题目内容
已知函数f（t）=|t+1|﹣|t﹣3|．
（I）求f（t）＞2的解集；
（II）设a＞0，g（x）=ax2﹣2x﹣5．若对任意实数x，t，均有g（x）≥f（t）恒成立，求a的取值范围．
考点：
函数恒成立问题；绝对值不等式的解法．
专题：
计算题．
分析：
（I）找出界点t=﹣1和t=3，分三种情况进行讨论，将问题转化为求解不等式问题；
（II）根据题意对任意实数x，t，均有g（x）≥f（t）恒成立，将问题转化为g（x）的最小值大于等于f（t）的最大值即可；
解答：
解：（I）由|t+1|﹣|t﹣3|＞2得，
（1）当t＜﹣1，时
可得﹣4＞2，t∈∅；
（2）当﹣1≤t≤3时，
2t﹣2＞2，解得{t|2＜t≤3}；
（3）当t＞3时，4＞2恒成立，
∴t＞2；
∴f（t）＞2的解集为{t|t＞2}；
（II）∵a＞0，g（x）=ax2﹣2x+5，g（x）≥f（t）恒成立，
可转化为gmin（x）≥fmax（t）
g（x）=a（x﹣
）2+
f（t）=|t﹣1|﹣|t﹣3|≤|t+1﹣t+3|=4，
∴
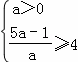解得a≥1；
点评：
此题考查绝对值不等式求解问题和函数的恒成立转化问题，考查的知识点比较全面，是一道中档题；
练习册系列答案
相关题目