题目内容
已知函数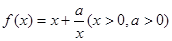 的图像如右所示。
的图像如右所示。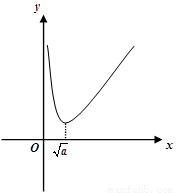
(1)求证: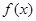 在区间
在区间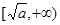 为增函数;
为增函数;
(2)试讨论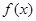 在区间
在区间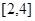 上的最小值.(要求把结果写成分段函数的形式)
上的最小值.(要求把结果写成分段函数的形式)
【答案】
(1)利用函数定义或者导数法来加以证明。
(2)根据第一问的结论,那么结合单调性来得到最值。
当 时,最小值
时,最小值
当 时,最小值
时,最小值
当 时,最小值
时,最小值
【解析】
试题分析:解:(1)根据题,由于 ,当f’(x)>0,得到的x的取值集合为
,当f’(x)>0,得到的x的取值集合为 ,可知函数在区间
,可知函数在区间 为增函数
为增函数
(2)由上可知,那么需要对于参数a进行分情况讨论,
当 时,函数在区间
时,函数在区间 递减,则可知在x=4处取得最小值
递减,则可知在x=4处取得最小值
当 时,函数在区间
时,函数在区间 递减,
递减, 在递增,则可知在x=
在递增,则可知在x= 处取得最小值
处取得最小值 .
.
当 时,函数在区间
时,函数在区间 递增,则可知在x=2处取得最小值
递增,则可知在x=2处取得最小值
考点:函数单调性
点评:主要是考查了函数单调性的定义以及运用,属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
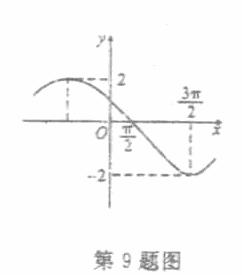
 的图像如右图所示,则
的图像如右图所示,则 .
.
 的图像如图所示,则把函数
的图像如图所示,则把函数 图像向右平移
图像向右平移 个单位所对应的函数解析式为 ( )
个单位所对应的函数解析式为 ( )
 B.
B.
 D.
D.
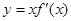 的图像如右图所示(其中
的图像如右图所示(其中 是函数
是函数 ,
,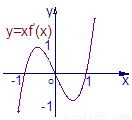 下面四个图象中
下面四个图象中 的图象大致是__________;
的图象大致是__________;