题目内容
已知函数f(x)=Asin(2ωx+φ)(A,ω>0,0<φ<π)在x= 时取最大值2,x1,x2是集合M={x∈R|f(x)=0}中的任意两个元素,且|x1-x2|的最小值为
时取最大值2,x1,x2是集合M={x∈R|f(x)=0}中的任意两个元素,且|x1-x2|的最小值为 .
.
(1)求f(x);
(2)若f(a)= ,a∈(
,a∈( ,
, ),求sin(
),求sin( -2a)的值.
-2a)的值.
解:(1)由已知得:A=2,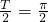 所以T=π,2ω=2从而ω=1;
所以T=π,2ω=2从而ω=1;
且sin(2× x+φ)=1 结合0<φ<π知φ=
x+φ)=1 结合0<φ<π知φ= 所以函数f(x)=2sin(2x+
所以函数f(x)=2sin(2x+ )
)
(2)由f(a)= ,得sin(2x+
,得sin(2x+ )=
)=
因a∈( ,
, ),所以
),所以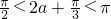
所以cos(2a+ )=
)=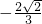
于是sin( -2a)=sin[
-2a)=sin[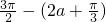 ]
]
=-cos(2a+ )=
)=
分析:(1)利用函数的最大值求出A,|x1-x2|的最小值为 .求出函数的周期,得到ω,利用x=
.求出函数的周期,得到ω,利用x= 时取最大值2,结合0<φ<π,求出φ,求出函数f(x)的表达式;
时取最大值2,结合0<φ<π,求出φ,求出函数f(x)的表达式;
(2)通过f(a)= ,a∈(
,a∈( ,
, ),求出cos(2a+
),求出cos(2a+ ),利用诱导公式化简sin(
),利用诱导公式化简sin( -2a),得到cos(2a+
-2a),得到cos(2a+ )的形式,从而求出表达式的值.
)的形式,从而求出表达式的值.
点评:本题是中档题,考查函数的解析式的求法,注意周期的应用,诱导公式的化简是简化(2)的关键,考查计算能力.
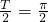 所以T=π,2ω=2从而ω=1;
所以T=π,2ω=2从而ω=1;且sin(2×
 x+φ)=1 结合0<φ<π知φ=
x+φ)=1 结合0<φ<π知φ= 所以函数f(x)=2sin(2x+
所以函数f(x)=2sin(2x+ )
)(2)由f(a)=
 ,得sin(2x+
,得sin(2x+ )=
)=
因a∈(
 ,
, ),所以
),所以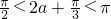
所以cos(2a+
 )=
)=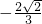
于是sin(
 -2a)=sin[
-2a)=sin[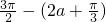 ]
]=-cos(2a+
 )=
)=
分析:(1)利用函数的最大值求出A,|x1-x2|的最小值为
 .求出函数的周期,得到ω,利用x=
.求出函数的周期,得到ω,利用x= 时取最大值2,结合0<φ<π,求出φ,求出函数f(x)的表达式;
时取最大值2,结合0<φ<π,求出φ,求出函数f(x)的表达式;(2)通过f(a)=
 ,a∈(
,a∈( ,
, ),求出cos(2a+
),求出cos(2a+ ),利用诱导公式化简sin(
),利用诱导公式化简sin( -2a),得到cos(2a+
-2a),得到cos(2a+ )的形式,从而求出表达式的值.
)的形式,从而求出表达式的值.点评:本题是中档题,考查函数的解析式的求法,注意周期的应用,诱导公式的化简是简化(2)的关键,考查计算能力.

练习册系列答案
相关题目