题目内容
有一枚正方体骰子,六个面分别写1、2、3、4、5、6的数字,规定“抛掷该枚骰子得到的数字是抛掷后,面向上的那一个数字”.已知 和
和 是先后抛掷该枚骰子得到的数字,函数
是先后抛掷该枚骰子得到的数字,函数

(1)若先抛掷骰子得到的数字是3,求再次抛掷骰子时,使函数 有零点的概率;
有零点的概率;
(2)求函数 在区间(-3,+∞)上是增函数的概率.
在区间(-3,+∞)上是增函数的概率.
(1) (2)
(2)
解析试题分析:(1)解:设事件A:再次抛掷骰子时,函数 有零点.
有零点.
若 有零点,则
有零点,则
 .所以
.所以 .
.
答:再次抛掷骰子时,函数 有零点的概率为
有零点的概率为 .
.
(2)解:设事件B为函数 在
在 为增函数.
为增函数.
若函数 在
在 上是增函数,则有
上是增函数,则有 ,即
,即 .
.
当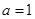 时,
时, ;当
;当 时,
时, .所以
.所以
答:函数 在
在 上是增函数的概率是
上是增函数的概率是 .
.
考点:概率公式;二次函数图象上点的坐标特征.
点评:本题巧妙地把概率、不等式组、二次函数等知识结合在一起,出题思路新颖,别具-格.有利于考查学生灵活应用基础知识解决问题的能力.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
 ,
, ,函数
,函数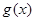 的图像在点
的图像在点 处的切线平行于
处的切线平行于 轴.
轴. 的值;
的值; 的直线与函数
的直线与函数 的图象交于两点
的图象交于两点 ,(
,( )
) .
. ,
, .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 在区间
在区间 上是减函数,求
上是减函数,求 的取值范围.
的取值范围. 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点 处的切线的斜率是
处的切线的斜率是 .
. 的值;
的值; 在区间
在区间 上的最大值;
上的最大值; ,曲线
,曲线 上是否存在两点
上是否存在两点 ,使得
,使得 是以
是以
 时,求
时,求 在[1,
在[1, ]上的取值范围。
]上的取值范围。 在[1,
在[1, ,
, ,
,
 与曲线
与曲线 相交,且在交点处有相同的切线,求
相交,且在交点处有相同的切线,求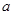 的值及该切线的方程;
的值及该切线的方程; ,当
,当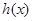 存在最小值时,求其最小值
存在最小值时,求其最小值 的解析式;
的解析式; 时,
时,  .
. ,函数
,函数
 求
求 的值;
的值; 的最大值和单调递增区间。
的最大值和单调递增区间。 的定义域为
的定义域为 ,且满足对于定义域内任意的
,且满足对于定义域内任意的 都有等式
都有等式 .
. 的值;
的值; ,且
,且 上是增函数,解关于
上是增函数,解关于 的不等式
的不等式 .
.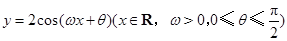 的图象与
的图象与 轴相交于点
轴相交于点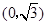 ,且该函数的最小正周期为
,且该函数的最小正周期为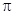 .
.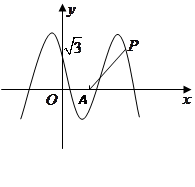
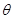 和
和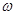 的值;
的值;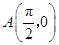 ,点
,点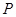 是该函数图象上一点,
是该函数图象上一点,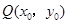 是
是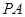 的中点,当
的中点,当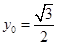 ,
,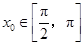 时,求
时,求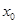 的值.
的值.