题目内容
要在如下表所示的5×5正方形的25个空格中填入自然数,使得每一行,每一列的数都成等差数列.
则x,y的值分别为( )
| ※ | ||||
| 74 | ||||
| 2y | 186 | |||
| y | 103 | |||
| 0 | x | 2x |
分析:根据题意以及等差数列的定义和性质,等差数列的通项公式,用2种方法求得a33,得到2x+y=113 ①.用2种方法求得a23,可得2×74-3y=2y+83 ②.再由①②联立方程组,解方程组求得x,y的值.
解答:解:设aij表示第i行第j列的数,则a52=x,a41=y,由第3行 a33=
=93+y,
由第3列 a33=2×103-2x,可得93+y=206-2x,即2x+y=113 ①.
又由第2行:a23=2×74-3y,
由第3列 a23=2a33-103=2y+83,∴2×74-3y=2y+83 ②.
根据①②解得y=13,故x=50,
故选C.
| 2y+186 |
| 2 |
由第3列 a33=2×103-2x,可得93+y=206-2x,即2x+y=113 ①.
又由第2行:a23=2×74-3y,
由第3列 a23=2a33-103=2y+83,∴2×74-3y=2y+83 ②.
根据①②解得y=13,故x=50,
故选C.
点评:本题主要考查等差数列的定义和性质,等差数列的通项公式的应用,属于中档题.

练习册系列答案
相关题目
(本小题满分12分)
国家教育部、体育总局和共青团中央曾共同号召,在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动为此某网站于2010年1月18日至24日,在全国范围内进行了持续一周的在线调查,随机抽取其中200名大中小学生的调查情况,就每天的睡眠时间分组整理如下表所示:
|
序号( |
每天睡眠时间 (小时) |
组中值( |
频数 |
频率 ( |
|
1 |
[4,5) |
4.5 |
8 |
0.04 |
|
2 |
[5,6) |
5.5 |
52 |
0.26 |
|
3 |
[6,7) |
6.5 |
60 |
0.30 |
|
4 |
[7,8) |
7.5 |
56 |
0.28 |
|
5 |
[8,9) |
8.5 |
20 |
0.10 |
|
6 |
[9,10) |
9.5 |
4 |
0.02 |
(Ⅰ)估计每天睡眠时间小于8小时的学生所占的百分比约是多少?
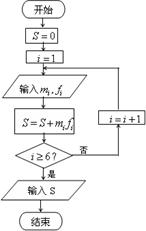
(Ⅱ)该网站利用右边的算法流程图,对样本数据作进一步统计分析,求输出的S的值,并说明S的统计意义。
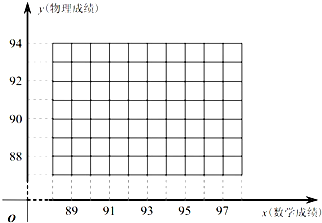 (2013•深圳一模)一次考试中,五名学生的数学、物理成绩如下表所示:
(2013•深圳一模)一次考试中,五名学生的数学、物理成绩如下表所示:
 )
) )
) )
)