题目内容
5.已知9x+4y=1,求3x-1+22y-1的最大值.分析 根据条件得出4y=1-(3x)2,运用指数幂得出m=3x-1+22y-1=$\frac{1}{3}$×3x+$\frac{1}{2}×$4x=$\frac{1}{3}×{3}^{x}$$+\frac{1}{2}×$(1-(3x)2)=-$\frac{1}{2}×$(3x)2$+\frac{1}{3}×{3}^{x}$$+\frac{1}{2}$,整体转化为二次函数求解即可.
解答 解:∵9x+4y=1,
∴4y=1-(3x)2,
∴m=3x-1+22y-1=$\frac{1}{3}$×3x+$\frac{1}{2}×$4x=$\frac{1}{3}×{3}^{x}$$+\frac{1}{2}×$(1-(3x)2)=-$\frac{1}{2}×$(3x)2$+\frac{1}{3}×{3}^{x}$$+\frac{1}{2}$
设t=3x,
∴m=$-\frac{1}{2}{t}^{2}$$+\frac{1}{3}t$$+\frac{1}{2}$,
当t=$\frac{1}{3}$时,m最大值为:$-\frac{1}{2}×\frac{1}{9}$$+\frac{1}{9}$$+\frac{1}{2}$=$\frac{10}{18}$=$\frac{5}{9}$
点评 本题考查了运用函数思想转化求解代数式的范围问题,属于中档题,关键是指数幂的化简运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.若x.y满足约束条件$\left\{\begin{array}{l}{x+y≥1}\\{x-y≥-1}\\{2x-y≤2}\end{array}\right.$,若目标函数z=ax+3y仅在点(1,0)处取得最小值,则实数a的取值范围为( )
| A. | (-3,6)) | B. | (3,6) | C. | (-6,3)) | D. | [-3,6] |
16.已知函数$f(x)=\left\{{\;}\right._{2f(x-2),x∈(0,+∞)}^{1-|x+1|,x∈[-2,0]}$,则下列说法中错误的是( )
| A. | f(x)的单调递减区间为[2n-3,2n-2](n∈N*) | |
| B. | f(x)的值域为[0,+∞) | |
| C. | 方程f(x)=1在区间[-2,2n]上所有根的个数为2n+1(n∈N) | |
| D. | 若方程f(x)=x+2在区间[-2,4]内有3个不等实根,则实数的取值范围是-2<a≤0 |
14.已知函数y-1=logax,则该函数恒过定点( )
| A. | (0,1) | B. | (1,1) | C. | (1,-1) | D. | (1,0) |
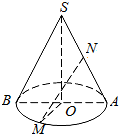 已知圆锥的底面半径r=2,半径OM与母线SA垂直,N是SA中点,NM与高SO所成的角为α,tanα=2.则圆锥的体积为$\frac{4\sqrt{5}}{3}π$.
已知圆锥的底面半径r=2,半径OM与母线SA垂直,N是SA中点,NM与高SO所成的角为α,tanα=2.则圆锥的体积为$\frac{4\sqrt{5}}{3}π$.