题目内容
（本题满分12分）设函数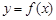
，对任意实数
都有
（Ⅰ）求
的值；
（Ⅱ）若
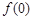的值；
（Ⅲ）在（Ⅱ）的条件下，猜想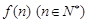
的表达式，并用数学归纳法加以证明.
【答案】
（Ⅰ）
（Ⅱ）
（Ⅲ）
证明如下：（1）当
时，
，猜想成立
（2）假设
时猜想成立，即
则
所以当
时，猜想也成立
综合（1）（2）可知，对一切
，都有
成立.
【解析】解：（Ⅰ）令
得：…… 2分
（Ⅱ）由
…… 4分
（Ⅲ）由（Ⅱ）猜想
…… 6分
证明如下：（1）当时，，猜想成立
…… 7分
（2）假设时猜想成立，即
…… 8分
则 …… 10分
所以当时，猜想也成立
…… 11分
综合（1）（2）可知，对一切，都有成立.
……12分
练习册系列答案
相关题目
:实数
满足
, 命题
:实数
.
为真，求实数
.
的单调区间；
对
恒成立，求实数
的取值范围.
,其中
。
时，求不等式
的解集；
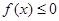的解集为
，求a的值。
与
垂直，求
的值 
的最大值; 
,
分别是椭圆
：
的左、右焦点，过
与
、
两点，且
，
，
成等差数列，
满足
,求