题目内容

已知
a
=(x2，1)，
b
=(t，
1
x2+1
)，且
a
||
b
，则实数t的取值范围为
[0，1）
[0，1）
．
分析：根据题意，有
a
∥
b
，根据向量平行的充要条件，构造等式，最后表示出t，利用函数的值值即可得到答案．
解答：解：∵且
a
||
b
，
∴x2 •
1
x2+1
-t=0，
即t=
x 2
x2+1
∈[0，1），
故答案为：[0，1）．
点评：本题主要考查的知识点是向量平行的坐标运算：
a
=(x1，y1)，
b
=(x2，y2)，则
a
∥
b
?x1•y2-x2y1=0
练习册系列答案
相关题目
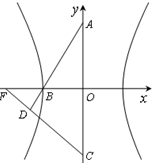精英家教网如图，已知双曲线x2-
y2
3
=1，A，C分别是虚轴的上、下顶点，B是左顶点，F为左焦点，直线AB与FC相交于点D，则∠BDF的余弦值是（　　）
A、
7
7
B、
5
7
7
C、
7
14
D、
5
7
14
下列是有关直线与圆锥曲线的命题：
①过点（2，4）作直线与抛物线y2=8x有且只有一个公共点，这样的直线有2条；
②过抛物线y2=4x的焦点作一条直线与抛物线相交于A，B两点，它们的横坐标之和等于5，则这样的直线有且仅有两条；
③过点（3，1）作直线与双曲线
x2
4
-y2=1有且只有一个公共点，这样的直线有3条；
④过双曲线x2-
y2
2
=1的右焦点作直线l交双曲线于A，B两点，若|AB|=4，则满足条件的直线l有3条；
⑤已知双曲线x2-
y2
2
=1和点A（1，1），过点A能作一条直线l，使它与双曲线交于P，Q两点，且点A恰为线段PQ的中点．
其中说法正确的序号有
①②④
①②④
．（请写出所有正确的序号）
（2012•西城区二模）已知双曲线x2-ky2=1的一个焦点是(
5
，0)，则其渐近线的方程为（　　）
已知
a
=(x2，1)，
b
=(t，
1
x2+1
)，且
a
||
b
，则实数t的取值范围为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网