Question

【题目】已知椭圆E的长轴长与焦距比为2：1，左焦点F（﹣2，0），一定点为P（﹣8，0）．

（1）求椭圆E的标准方程；

（2）过P的直线与椭圆交于P1、P2两点，设直线P1F、P2F的斜率分别为k1、k2，求证：k1+k2=0．

（3）求△P1P2F面积的最大值．

Answer 1

【答案】（1）+=1；（2）见解析;（3）3．

【解析】

（1）设椭圆方程为+=1（a＞b＞0），

由题意可得c=2，e==，又c2=a2﹣b2，

解得c=2，a=4，b=2，

即椭圆方程为+=1；

（2）证明：设直线P1P2：y=k（x+8），

代入椭圆方程可得（3+4k2）x2+64k2x+256k2﹣48=0，

由△=642k4﹣4（3+4k2）（256k2﹣48）＞0，即有

设P1（x1，y1），P2（x2，y2），

x1+x2=﹣，x1x2=，

即有k1+k2=+=+=k，

将韦达定理代入上式，可得

2x1x2+10（x1+x2）+32=﹣+32=0，

则k1+k2=0；

（2）△P1P2F面积S=|PF||y1﹣y2|

=3|k||x1﹣x2|=3|k|=3|k|

=72，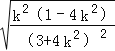

设t=3+4k2（3＜t＜4），

则S=72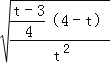=36=36，

当=即t=即k=±时，取得最大值，且为3．

则△P1P2F面积的最大值为3．