题目内容
数列{an}的前n项和为Sn,a1=1,an+1-an-1=0,数列{bn}满足b1=2,anbn+1=2an+1bn.
(1)求S200; (2)求bn.
解:(1)∵{an}的前n项和为Sn,a1=1,an+1-an-1=0,
∴an+1-an=1,
∴数列{an}是以a1=1为首项,d=1为公差的等差数列,
∴S200= .
.
(2)由(1)得an=n,
∵数列{bn}满足b1=2,anbn+1=2an+1bn,
∴nbn+1=2(n+1)bn,
∴ ,
,
∴{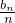 }是以
}是以 =2为首项,q=2为公比的等比数列,
=2为首项,q=2为公比的等比数列,
∴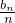 =2×2n-1=2n,
=2×2n-1=2n,
∴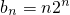 .
.
分析:(1)由{an}的前n项和为Sn,a1=1,an+1-an-1=0,知数列{an}是以a1=1为首项,d=1为公差的等差数列,由此能求出S200.
(2)由an=n,数列{bn}满足b1=2,anbn+1=2an+1bn,知nbn+1=2(n+1)bn,所以 ,由此知{
,由此知{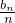 }是以
}是以 =2为首项,q=2为公比的等比数列,由此能求出bn.
=2为首项,q=2为公比的等比数列,由此能求出bn.
点评:本题考查等差数列、等比数列的基本量、通项,结合含两个变量的不等式的处理问题,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意合理地进行等价转化.
∴an+1-an=1,
∴数列{an}是以a1=1为首项,d=1为公差的等差数列,
∴S200=
 .
.(2)由(1)得an=n,
∵数列{bn}满足b1=2,anbn+1=2an+1bn,
∴nbn+1=2(n+1)bn,
∴
 ,
,∴{
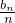 }是以
}是以 =2为首项,q=2为公比的等比数列,
=2为首项,q=2为公比的等比数列,∴
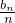 =2×2n-1=2n,
=2×2n-1=2n,∴
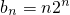 .
.分析:(1)由{an}的前n项和为Sn,a1=1,an+1-an-1=0,知数列{an}是以a1=1为首项,d=1为公差的等差数列,由此能求出S200.
(2)由an=n,数列{bn}满足b1=2,anbn+1=2an+1bn,知nbn+1=2(n+1)bn,所以
 ,由此知{
,由此知{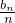 }是以
}是以 =2为首项,q=2为公比的等比数列,由此能求出bn.
=2为首项,q=2为公比的等比数列,由此能求出bn.点评:本题考查等差数列、等比数列的基本量、通项,结合含两个变量的不等式的处理问题,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目