题目内容
若loga2=m,loga5=n,则a3m+n=
- A.11
- B.13
- C.30
- D.40
D
分析:由已知中loga2=m,loga5=n,我们根据指数式与对数式的转化方法,可得am=2,an=5,进而根据指数的运算性质,am+n=am•an,amn=(am)n,可计算出a3m+n的值.
解答:∵loga2=m,loga5=n,
∴am=2,an=5
∴a3m+n=a3m•an=23•5=40
故选D
点评:本题考查的知识点是对数的运算性质,及指数的运算性质,其中根据指数式与对数式的转化方法,将已知转化为am=2,an=5,将问题转化为指数运算,是解答本题的关键.
分析:由已知中loga2=m,loga5=n,我们根据指数式与对数式的转化方法,可得am=2,an=5,进而根据指数的运算性质,am+n=am•an,amn=(am)n,可计算出a3m+n的值.
解答:∵loga2=m,loga5=n,
∴am=2,an=5
∴a3m+n=a3m•an=23•5=40
故选D
点评:本题考查的知识点是对数的运算性质,及指数的运算性质,其中根据指数式与对数式的转化方法,将已知转化为am=2,an=5,将问题转化为指数运算,是解答本题的关键.

练习册系列答案
相关题目

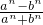 =1(其中n∈N+);
=1(其中n∈N+);
 =1(其中n∈N+);
=1(其中n∈N+);