题目内容
直线y=kx+b与曲线y=ax2+2+lnx相切于点P（1，4），则b的值为（ ）
分析：把切点P的坐标代入y=ax2+2+lnx求出a，再求函数导数并求出k，再把P（1，4）代入y=kx+b求b．
解答：解：∵点P（1，4）在曲线y=ax2+2+lnx上，
∴a+2=4，解得a=2，
由题意得，y′=2ax+
=4x+
，
∴在点P（1，4）处的切线斜率k=5，
把P（1，4）代入y=kx+b，得b=-1，
故选C．
∴a+2=4，解得a=2，
由题意得，y′=2ax+
| 1 |
| x |
| 1 |
| x |
∴在点P（1，4）处的切线斜率k=5，
把P（1，4）代入y=kx+b，得b=-1，
故选C．
点评：本题考查了导数的几何意义，某点处的切线的斜率是该点处的导数值，及切点在曲线上和切线上的应用．
练习册系列答案
相关题目
或2
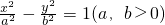的虚轴长为2
，渐近线方程是y=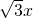
，O为坐标原点，直线y=kx+m（k，m∈R）与双曲线C相交于A、B两点，且
．
的虚轴长为2
，渐近线方程是y=
，O为坐标原点，直线y=kx+m（k，m∈R）与双曲线C相交于A、B两点，且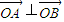
．