题目内容
在Rt△ABC,∠C=90°中,且∠A、∠B、∠C所对边分别为a,b,c,若a+b=cx,则实数x的取值范围为
(1,
)
| 2 |
(1,
)
.| 2 |
分析:由∠C=90°,得到sinC=1,然后利用正弦定理表示出a与b,代入a+b=cx,表示出x,利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,由A的范围求出这个角的范围,从而根据正弦函数的图象与性质得到正弦函数的值域,得到x的范围.
解答:解:∵∠C=90°,∴sinC=1,
∴由正弦定理得:
=
=
=c,
∴a=csinA,b=csinB,
∴a+b=csinA+csinB=cx,即sinA+sinB=x,
又A+B=90°,即B=90°-A,
∴sinB=sin(90°-A)=cosA,
则x=sinA+sinB=sinA+cosA=
(
sinA+
cosA)=
sin(A+
),
∵
<A+
<
,
∴sin(A+
)∈(
,1),
∴
sin(A+
)∈(1,
),
则x∈(1,
).
故答案为:(1,
)
∴由正弦定理得:
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∴a=csinA,b=csinB,
∴a+b=csinA+csinB=cx,即sinA+sinB=x,
又A+B=90°,即B=90°-A,
∴sinB=sin(90°-A)=cosA,
则x=sinA+sinB=sinA+cosA=
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
∵
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴sin(A+
| π |
| 4 |
| ||
| 2 |
∴
| 2 |
| π |
| 4 |
| 2 |
则x∈(1,
| 2 |
故答案为:(1,
| 2 |
点评:此题属于解三角形的题型,涉及的知识有正弦定理,两角和与差的正弦函数公式,正弦函数的定义域与值域,以及特殊角的三角函数值,其中根据正弦定理表示出a与b是本题的突破点.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目



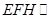 平面
平面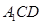 ,分别交CB于F,
,分别交CB于F,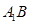 于H,求截面
于H,求截面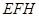 的面积;
的面积;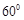 的角?说明理由.
的角?说明理由.