题目内容
已知函数f(x)=-x3+ax2-4.
(1) 若f(x)在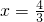 处取得极值,求实数a的值;
处取得极值,求实数a的值;
(2) 在(Ⅰ)的条件下,若关于x的方程f(x)=m在[-1,1]上恰有两个不同的实数根,求实数m的取值范围;
(3) 若存在x0∈(0,+∞),使得不等式f(x0)>0成立,求实数a的取值范围.
 (1)f'(x)=-3x2+2ax,由题意得
(1)f'(x)=-3x2+2ax,由题意得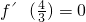 ,解得a=2,经检验满足条件.
,解得a=2,经检验满足条件.(2)由(1)知f(x)=-x3+2x2-4,f'(x)=-3x2+4x,
令f'(x)=0,则x1=0,
 (舍去).f'(x),f(x)的变化情况如下表:
(舍去).f'(x),f(x)的变化情况如下表:| x | -1 | (-1,0) | 0 | (0,1) | 1 |
| f'(x) | - | 0 | + | ||
| f(x) | -1 | ↘ | -4 | ↗ | -3 |
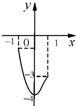
∴f(x)极小值=f(0)=-4,如图构造f(x)在[-1,1]上的图象.
又关于x的方程f(x)=m在[-1,1]上恰有两个不同的实数根,
则-4<m≤-3,即m的取值范围是(-4,-3].
(3)解法一:因存在x0∈(0,+∞),使得不等式f(x0)>0成立,
故只需要f(x)的最大值f(x)max>0即可,
∵f(x)=-x3+ax2-4,∴
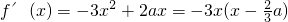 .
.①若a≤0,则当x>0时,f'(x)<0,∴f(x)在(0,+∞)单调递减.
∵f(0)=-4<0,∴当x>0时,f(x)<-4<0,
∴当a≤0时,不存在x0∈(0,+∞),使得不等式f(x0)>0成立.
②当a>0时f(x),f'(x)随x的变化情况如下表:
| x | 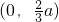 | 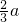 | 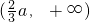 |
| f'(x) | + | 0 | - |
| f(x) | ↗ | 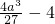 | ↘ |
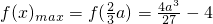 ,由
,由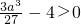 得a>3.
得a>3.综上得a>3,即a的取值范围是(3,+∞).
解法二:根据题意,只需要不等式f(x)>0在(0,+∞)上有解即可,
即-x3+ax2-4>0在(0,+∞)上有解.即不等式
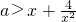 在(0,+∞)上有解即可.
在(0,+∞)上有解即可.令
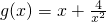 ,只需要a>g(x)min
,只需要a>g(x)min而
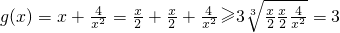 ,当且仅当
,当且仅当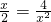 ,即x=2时“=”成立.
,即x=2时“=”成立.故a>3,即a的取值范围是(3,+∞).
分析:(1)首先利用函数的导数与极值的关系求出a的值,(2)在(Ⅰ)的条件下,若关于x的方程f(x)=m在[-1,1]上恰有两个不同的实数根,即函数f(x)的图象与直线y=m有两个交点,利用导数即求函数f(x)在区间[-1,1]上的最值;(3)解法一:存在x0∈(0,+∞),使f(x0)>0即寻找f(x)max>0是变量a的范围;解法二:存在x0∈(0,+∞),使得不等式f(x0)>0成立,即即-x3+ax2-4>0在(0,+∞)上有解,分离参数,即求a>g(x)min,转化为求函数的最小值.
点评:此题是个难题.考查利用导数研究函数的极值、单调性和最值问题,体现了数形结合和转化的思想方法.其中问题(3)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|