题目内容
1.在![]() 中,
中,![]() ,
,![]() .
.
(1)求角![]() ;
;
(2)设![]() ,求
,求![]() 的面积.
的面积.
(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
解析:
(Ⅰ)由![]() ,
,![]() ,得
,得![]() ,所以
,所以![]() ,
,![]() ,
,
因为![]() ,
,
且![]() , 故
, 故![]() . w.w.w.k.s.5.u.c.o.m
. w.w.w.k.s.5.u.c.o.m
(Ⅱ)根据正弦定理得![]() ,
,
所以![]() 的面积为
的面积为![]() .
.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
(本小题满分12分)
某市为了对学生的数理(数学与物理)学习能力进行分析,从10000名学生中随机抽出100位学生的数理综合学习能力等级分数(6分制)作为样本,分数频数分布如下表:
|
等级得分 |
|
|
|
|
|
|
|
人数 |
3 |
17 |
30 |
30 |
17 |
3 |
(Ⅰ)如果以能力等级分数大于4分作为良好的标准,从样本中任意抽取2名学生,求恰有1名学生为良好的概率;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值(例如区间 的中点值为1.5)作为代表:
的中点值为1.5)作为代表:
(ⅰ)据此,计算这100名学生数理学习能力等级分数的期望 及标准差
及标准差 (精确到0.1);
(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,估计该市这10000名学生中数理学习能力等级在 范围内的人数 .
范围内的人数 .
(Ⅲ)从这10000名学生中任意抽取5名同学,
他们数学与物理单科学习能力等级分
数如下表:


(ⅰ)请画出上表数据的散点图;
(ⅱ)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程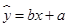 (附参考数据:
(附参考数据: )
)
 (3)从这些学生中任选两名学生,用
(3)从这些学生中任选两名学生,用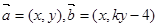 (
(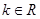 ),
),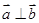 ,动点
,动点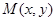 的轨迹为
的轨迹为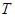 .
.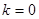 时,过点
时,过点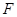 (0,1),作轨迹T的两条互相垂直的弦
(0,1),作轨迹T的两条互相垂直的弦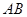 、
、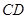 ,设
,设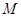 、
、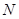 ,试判断直线
,试判断直线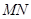 是否过定点?并说明理由.
是否过定点?并说明理由.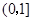





 中,
中,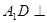 平面
平面 ,底面
,底面 的正方形,侧棱
的正方形,侧棱 .
.
 的体积;
的体积; 与平面
与平面 所成角的正弦值;
所成角的正弦值; 上存在一点
上存在一点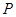 ,使得
,使得 ,当二面角
,当二面角 的大小为
的大小为 时,求实数
时,求实数 的值.
的值. 中,
中,
 .
(3’)
.
(3’) ,则
,则 (4’)
(4’) ,设平面
,设平面 ,
,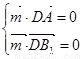 得
得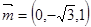 ,
(5’)
,
(5’) ,
,  . (7’)
. (7’)
 的法向量为
的法向量为 ,由
,由 得
得 ,
(10’)
,
(10’)