题目内容
椭圆与双曲线有许多优美的对偶性质,对于椭圆有如下命题:已知A,F,B分别是优美椭圆![]() +
+![]() =1(a>b>0)(离心率为黄金分割比
=1(a>b>0)(离心率为黄金分割比![]() 的椭圆)的左顶点、右焦点和上顶点,则AB⊥BF,那么对于双曲线则有如下命题:已知A,F,B分别是优美双曲线
的椭圆)的左顶点、右焦点和上顶点,则AB⊥BF,那么对于双曲线则有如下命题:已知A,F,B分别是优美双曲线![]() -
-![]() =1(a>0,b>0)(离心率为黄金分割比的倒数
=1(a>0,b>0)(离心率为黄金分割比的倒数![]() 的双曲线)的左顶点、右焦点和其虚轴的上端点,则有
的双曲线)的左顶点、右焦点和其虚轴的上端点,则有
[ ]
A.
AB⊥BF
B.
AF⊥BF
C.
AB⊥AF
D.
AB∥BF
答案:A
解析:
解析:
|
根据类比推理的方法可以得到结论AB⊥BF,也可利用双曲线的相关知识进行证明. |

练习册系列答案
相关题目
 +
+ =1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=-
=1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=- .那么对于双曲线则有如下命题:AB是双曲线
.那么对于双曲线则有如下命题:AB是双曲线 -
- =1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= .
=1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= .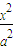 +
+ =1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=-
=1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=- .那么对于双曲线则有如下命题:AB是双曲线
.那么对于双曲线则有如下命题:AB是双曲线 -
- =1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= .
=1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= . +
+ =1(a>b>0)(离心率为黄金分割比
=1(a>b>0)(离心率为黄金分割比 的椭圆)的左顶点、右焦点和上顶点,则AB⊥BF.那么对于双曲线则有如下命题:已知A、F、B分别是优美双曲线
的椭圆)的左顶点、右焦点和上顶点,则AB⊥BF.那么对于双曲线则有如下命题:已知A、F、B分别是优美双曲线 -
- =1(a>b>0)(离心率为黄金分割比的倒数
=1(a>b>0)(离心率为黄金分割比的倒数 的双曲线)的左顶点、右焦点和其虚轴的上端点,则有( )
的双曲线)的左顶点、右焦点和其虚轴的上端点,则有( )