题目内容
AB为⊙O中的一条长为4的弦,P为⊙O上的一动点,cos∠APB =
思路解析:因为AB为定值,要使S△APB最大,只要AB边上的高最大,所以P在弓形的最高点即可,又∠APB为定值,根据圆周角定理的推论,想到构造直角三角形,使其一锐角等于∠APB.
解法一:存在以A、P、B为顶点的面积最大的三角形.?
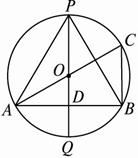
图2-1-12
∵cos∠APB=![]() ,∴∠APB≠90°.?
,∴∠APB≠90°.?
∴AB不是直径.?
过O作AB的垂线并延长,分别交优弧和劣弧的中点于P、Q,且PD、QD为弓形的高,?
∴P为优弧中点时,△APB面积最大,作⊙O直径AC,连结BC,?
则∠ABC =90°,∠APB=∠C,?
∴cos∠APB =cosC =![]() =
=![]() .?
.?
设BC=x,则AC =3x,?
在Rt△ABC中,AB =4,?
由勾股定理AC2 =AB2+BC2,?
∴(3x)2 =42+x2,解得x =![]() .?
.?
∴BC=![]() ,AC =3
,AC =3![]() .∴
.∴![]()
![]() .?
.?
∵AO =OC,AD =BD,∴![]()
![]() .?
.?
∴PD = PO + OD =![]() +
+![]() =
=![]() .?
.?
∴S△APB =![]() AB·PD =
AB·PD =![]() ×4×2
×4×2![]() =
=![]() .
.
解法二:同解法一,P为优弧中点时,△APB面积最大.?
作AC⊥PB,垂足为C,?
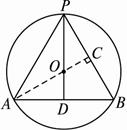
图2-1-13
在Rt△PCA中,cos∠APC=![]() ,?
,?
∴![]() =
=![]() .?
.?
设PC=x,则PA =PB =3x,AC =2![]() x,BC =2x,?
x,BC =2x,?
在Rt△ACB中,AB =4,?
由勾股定理得AC2+BC2=AB2,?
∴![]() +(2x)2=16,解得
+(2x)2=16,解得![]() .?
.?
∴AC =2![]() x=
x=![]() ,PB =3x =
,PB =3x =![]() .?
.?
∴S△PAB =PB·AC =![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 (理)已知函数
(理)已知函数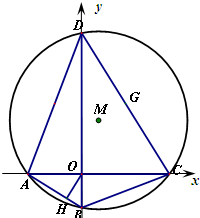 如图,在平面直角坐标系中,方程为x2+y2+Dx+Ey+F=0的圆M的内接四边形ABCD的对角线AC和BD互相垂直,且AC和BD分别在x轴和y轴上.
如图,在平面直角坐标系中,方程为x2+y2+Dx+Ey+F=0的圆M的内接四边形ABCD的对角线AC和BD互相垂直,且AC和BD分别在x轴和y轴上. 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤. =0,求D2+E2-4F的值;
=0,求D2+E2-4F的值;