题目内容
若函数y=loga（x+m）+n（a＞0，且a≠1）经过定点（3，-1），则m+n= ．
【答案】分析：根据对数的运算性质，1的对数恒为0（与底数无关），结合函数y=loga（x+m）+n（a＞0，且a≠1）经过定点（3，-1），可构造关于m，n的方程组，解方程组可得答案．
解答：解：若函数y=loga（x+m）+n恒过定点（3，-1），
即-1=loga（3+m）+n
则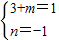
即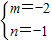
∴m+n=-3
故答案为：-3
点评：本题考查的知识点是对数函数的单调性与特殊点，其中熟练掌握对数的运算性质：1的对数恒为0（与底数无关），是解答本题的关键．
解答：解：若函数y=loga（x+m）+n恒过定点（3，-1），
即-1=loga（3+m）+n
则
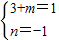
即
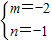
∴m+n=-3
故答案为：-3
点评：本题考查的知识点是对数函数的单调性与特殊点，其中熟练掌握对数的运算性质：1的对数恒为0（与底数无关），是解答本题的关键．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目