题目内容
已知函数f(x)=ax-a-x(a>0且a≠1).(I)证明函数f(x)是奇函数;
(II)讨论函数f(x)的单调性,并加以证明;
(III)是否存在实数a,使得函数f(x)在区间[1,2]上的最大值为
 ?若存在,求出a的值,若不存在请说明理由.
?若存在,求出a的值,若不存在请说明理由.
【答案】分析:(I)根据函数单调性的定义,直接加以验证即可得到函数f(x)是奇函数;
(II)设x1<x2,将f(x1)与f(x2)作差、因式分解,可得当a>1时f(x1)<f(x2),由定义可得函数f(x)是增函数,当0<a<1时f(x1)>f(x2),可得函数f(x)是减函数;
(III)分a>1时、0<a<1两种情况加以讨论,根据(II)中函数的单调性建立关于a的方程,解之可得存在
a=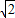 满足f(x)在区间[1,2]上的最大值为f(2)=
满足f(x)在区间[1,2]上的最大值为f(2)= .
.
解答:解:(I)∵f(x)=ax-a-x,
∴f(-x)=a-x-ax=-(ax-a-x)=-f(x)
因此,函数f(x)是奇函数;
(II)设x1<x2,可得
f(x1)-f(x2)=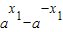 -(
-(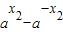 )=
)=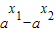 +
+
=(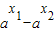 )(1+
)(1+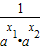 )
)
∵1+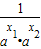 >0,当a>1时
>0,当a>1时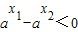 ,而0<a<1时
,而0<a<1时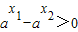
∴当a>1时f(x1)-f(x2)<0,函数f(x)是(-∞,+∞)上的增函数;
当0<a<1时f(x1)-f(x2)>0,函数f(x)是(-∞,+∞)上的减函数
(III)根据(II)的单调性,得
①当a>1时,f(x)在区间[1,2]上的最大值为f(2)=
即a2-a-2= ,解之得a2=2(舍负),所以a=
,解之得a2=2(舍负),所以a=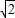 (舍负)
(舍负)
②当0<a<1时,f(x)在区间[1,2]上的最大值为f(1)=
即a1-a-1= ,解之得a=2不满足0<a<1,舍去
,解之得a=2不满足0<a<1,舍去
综上所述,可得存在a=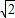 满足f(x)在区间[1,2]上的最大值为f(2)=
满足f(x)在区间[1,2]上的最大值为f(2)= .
.
点评:本题给出含有指数的基本初等函数,讨论函数的奇偶性、单调性并求函数在闭区间上的最值.着重考查了函数的奇偶性的定义、函数单调性的定义证明法和指数方程的解法等知识,属于中档题.
(II)设x1<x2,将f(x1)与f(x2)作差、因式分解,可得当a>1时f(x1)<f(x2),由定义可得函数f(x)是增函数,当0<a<1时f(x1)>f(x2),可得函数f(x)是减函数;
(III)分a>1时、0<a<1两种情况加以讨论,根据(II)中函数的单调性建立关于a的方程,解之可得存在
a=
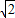 满足f(x)在区间[1,2]上的最大值为f(2)=
满足f(x)在区间[1,2]上的最大值为f(2)= .
.解答:解:(I)∵f(x)=ax-a-x,
∴f(-x)=a-x-ax=-(ax-a-x)=-f(x)
因此,函数f(x)是奇函数;
(II)设x1<x2,可得
f(x1)-f(x2)=
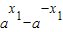 -(
-(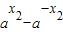 )=
)=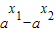 +
+
=(
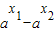 )(1+
)(1+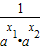 )
)∵1+
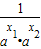 >0,当a>1时
>0,当a>1时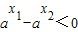 ,而0<a<1时
,而0<a<1时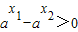
∴当a>1时f(x1)-f(x2)<0,函数f(x)是(-∞,+∞)上的增函数;
当0<a<1时f(x1)-f(x2)>0,函数f(x)是(-∞,+∞)上的减函数
(III)根据(II)的单调性,得
①当a>1时,f(x)在区间[1,2]上的最大值为f(2)=

即a2-a-2=
 ,解之得a2=2(舍负),所以a=
,解之得a2=2(舍负),所以a=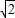 (舍负)
(舍负)②当0<a<1时,f(x)在区间[1,2]上的最大值为f(1)=

即a1-a-1=
 ,解之得a=2不满足0<a<1,舍去
,解之得a=2不满足0<a<1,舍去综上所述,可得存在a=
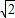 满足f(x)在区间[1,2]上的最大值为f(2)=
满足f(x)在区间[1,2]上的最大值为f(2)= .
.点评:本题给出含有指数的基本初等函数,讨论函数的奇偶性、单调性并求函数在闭区间上的最值.着重考查了函数的奇偶性的定义、函数单调性的定义证明法和指数方程的解法等知识,属于中档题.

练习册系列答案
相关题目