题目内容
函数f(x)对于任意实数x满足条件f(x+2)=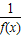 ,若f(1)=-5,则f[f(5)]= .
,若f(1)=-5,则f[f(5)]= .
【答案】分析:由已知中函数f(x)对于任意实数x满足条件f(x+2)=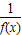 ,我们可确定函数f(x)是以4为周期的周期函数,进而根据周期函数的性质,从内到外依次去掉括号,即可得到答案.
,我们可确定函数f(x)是以4为周期的周期函数,进而根据周期函数的性质,从内到外依次去掉括号,即可得到答案.
解答:解:∵函数f(x)对于任意实数x满足条件f(x+2)=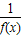 ,
,
∴f(x+4)=f[(x+2)+2]=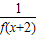 =
=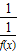 =f(x),
=f(x),
即函数f(x)是以4为周期的周期函数,
∵f(1)=-5
∴f[f(5)]=f[f(1)]=f(-5)=f(3)=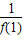 =
=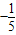
故答案为: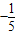
点评:本题考查的知识点是函数的周期性,函数的值,其中根据已知中函数f(x)对于任意实数x满足条件f(x+2)=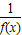 ,判断出函数f(x)是以4为周期的周期函数,是解答本题的关键.
,判断出函数f(x)是以4为周期的周期函数,是解答本题的关键.
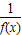 ,我们可确定函数f(x)是以4为周期的周期函数,进而根据周期函数的性质,从内到外依次去掉括号,即可得到答案.
,我们可确定函数f(x)是以4为周期的周期函数,进而根据周期函数的性质,从内到外依次去掉括号,即可得到答案.解答:解:∵函数f(x)对于任意实数x满足条件f(x+2)=
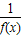 ,
,∴f(x+4)=f[(x+2)+2]=
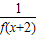 =
=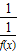 =f(x),
=f(x),即函数f(x)是以4为周期的周期函数,
∵f(1)=-5
∴f[f(5)]=f[f(1)]=f(-5)=f(3)=
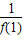 =
=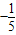
故答案为:
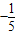
点评:本题考查的知识点是函数的周期性,函数的值,其中根据已知中函数f(x)对于任意实数x满足条件f(x+2)=
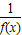 ,判断出函数f(x)是以4为周期的周期函数,是解答本题的关键.
,判断出函数f(x)是以4为周期的周期函数,是解答本题的关键. 
练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目