题目内容
给出下列命题:①若复平面内复数z=x-
i 所对应的点都在单位圆x2+y2=1内,则实数x的取值范围是-
<x<
;②在复平面内,若复数z满足|z-i|+|z+i|=4,则z在复平面内对应的点Z的轨迹是焦点在虚轴上的椭圆;③若z3=1,则复数z一定等于1;④若(x2-1)+(x2+3x+2)i是纯虚数,则实数x=±1,其中,正确命题的序号是
______
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
①∵若复平面内复数z=x-
i 所对应的点都在单位圆x2+y2=1内,
∴x2+
<1,
∴x2<
∴实数x的取值范围是-
<x<
∴①正确;
②在复平面内,若复数z满足|z-i|+|z+i|=4,
由复数的几何意义知,z到两个定点的距离之和是一个定值4
且4<2
∴z在复平面内对应的点Z的轨迹是焦点在虚轴上的椭圆;
∴②正确;
③若z3=1,则复数z一定等于1
当复数z是一个实数时,z=1,
当复数z是一个虚数时,z=-
±
i
∴③不正确;
④若(x2-1)+(x2+3x+2)i是纯虚数,
要满足x2-1=0,x2+3x+2≠0
而当x=-1时,x2+3x+2=0
∴④不正确.
故答案为:①②
| 1 |
| 2 |
∴x2+
| 1 |
| 4 |
∴x2<
| 3 |
| 4 |
∴实数x的取值范围是-
| ||
| 2 |
| ||
| 2 |
∴①正确;
②在复平面内,若复数z满足|z-i|+|z+i|=4,
由复数的几何意义知,z到两个定点的距离之和是一个定值4
且4<2
∴z在复平面内对应的点Z的轨迹是焦点在虚轴上的椭圆;
∴②正确;
③若z3=1,则复数z一定等于1
当复数z是一个实数时,z=1,
当复数z是一个虚数时,z=-
| 1 |
| 2 |
| ||
| 2 |
∴③不正确;
④若(x2-1)+(x2+3x+2)i是纯虚数,
要满足x2-1=0,x2+3x+2≠0
而当x=-1时,x2+3x+2=0
∴④不正确.
故答案为:①②

练习册系列答案
相关题目
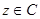 ,则
,则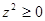 ;②若
;②若 ,且
,且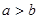 则
则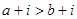 ③若
③若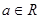 ,则
,则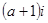 是纯虚数;④若
是纯虚数;④若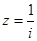 ,则
,则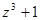 对应的点在复平面内的第一象限.其中正确命题的序号是 .
对应的点在复平面内的第一象限.其中正确命题的序号是 .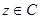 ,则
,则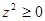 ;②若
;②若 ,且
,且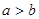 则
则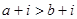
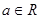 ,则
,则 是纯虚数;④若
是纯虚数;④若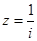 ,则
,则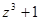 对应的点在复平面内的第一象限.其中正确命题的序号是 .
对应的点在复平面内的第一象限.其中正确命题的序号是 . ,则
,则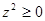 ;②若
;②若 ,且
,且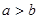 则
则 ;③若
;③若 ,则
,则 是纯虚数;④若
是纯虚数;④若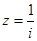 ,则
,则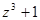 对应的点在复平面内的第一象限.其中正确命题的序号是 .
对应的点在复平面内的第一象限.其中正确命题的序号是 .