题目内容
已知p：0＜k＜2，q：方程
+
=1表示双曲线，若p∧q为真命题，求k的取值范围．
| x2 |
| k-1 |
| y2 |
| k-3 |
分析：若命题q为真命题，有（k-1）（k-3）＜0，由此能求出k的取值范围，再根据p∧q为真命题，得到p和q均为真命题，从而求得k的取值范围．
解答：解：若命题p为真命题，有0＜k＜2，
若命题p为真命题，有（k-1）（k-3）＜0，即1＜k＜3，
若p∧q为真命题，则若p和q都为真命题，
∴
，
∴1＜k＜2．
故所求的k的取值范围是1＜k＜2．
若命题p为真命题，有（k-1）（k-3）＜0，即1＜k＜3，
若p∧q为真命题，则若p和q都为真命题，
∴
|
∴1＜k＜2．
故所求的k的取值范围是1＜k＜2．
点评：本题考查命题的真假判断和应用，解题时要注意双曲线的性质的灵活应用．
练习册系列答案
相关题目
表示双曲线，若p∧q为真命题，求k的取值范围．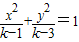
表示双曲线，若p∧q为真命题，求k的取值范围．