题目内容
19.己知x∈R,则函数f(x)=$\frac{x}{{x}^{2}+4}$的值域是[$-\frac{1}{4}$,$\frac{1}{4}$].分析 可设$y=\frac{x}{{x}^{2}+4}$,从而得到yx2+4y=x,进一步可得到yx2-x+4y=0,可看成关于x的方程,方程有解,显然需讨论y:y=0容易判断满足方程有解,而y≠0时,需满足△=1-16y2≥0,这样解出y的范围,并上y=0便可得出原函数的值域.
解答 解:设y=f(x),则:
yx2+4y=x;
∴yx2-x+4y=0,看成关于x的方程,方程有解;
①y=0时,x=0,满足方程有解;
②y≠0时,△=1-16y2≥0;
解得$-\frac{1}{4}≤y≤\frac{1}{4}$;
∴综上得,原函数的值域为$[-\frac{1}{4},\frac{1}{4}]$.
故答案为:[$-\frac{1}{4},\frac{1}{4}$].
点评 考查函数值域的概念,以及形如$y=\frac{a{x}^{2}+bx+c}{d{x}^{2}+ex+f}$的函数值域的求法:整理成关于x的方程的形式,根据方程有解求值域,一元二次方程有解时判别式△的取值情况.

练习册系列答案
相关题目
7.对于函数f(x)=$\frac{x-1}{x+1}$,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*,且n≥2),令集合M={x|f2015(x)=-x,x∈R},则集合M为( )
| A. | 空集 | B. | 实数集 | C. | 单元素集 | D. | 二元素集 |
7.设偶函数f(x)在[0,+∞)单调递增,则使得f(x)>f(2x-1)成立的x的取值范围是( )
| A. | ($\frac{1}{3}$,1) | B. | (-∞,$\frac{1}{3}$)∪(1,+∞) | C. | (-$\frac{1}{3}$,$\frac{1}{3}$) | D. | (-∞,-$\frac{1}{3}$)∪($\frac{1}{3}$,+∞) |
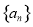 的前
的前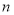 项和
项和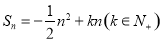 ,且
,且 的最大值为8.
的最大值为8.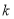 ,并求
,并求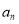 ;
;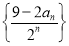 的前
的前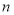 项和
项和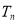 .
.