题目内容
某校有学生会干部7名,其中男干部有![]() ,A
,A![]() ,A
,A![]() ,A
,A![]() 共4人;女干部有B
共4人;女干部有B![]() ,B
,B![]() ,B
,B![]() 共3人.从中选出男、女干部各1名,组成一个小组参加某项活动.
共3人.从中选出男、女干部各1名,组成一个小组参加某项活动.
(Ⅰ)求A![]() 被选中的概率;
被选中的概率;
(Ⅱ)求A![]() ,B
,B![]() 不全被选中的概率.
不全被选中的概率.
解:(I)从7名学生会干部中选出男干部、女干部各1名,其一切可能的结果共有12种:
(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),
),
(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),
),
(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ).
).
用M表示“![]() 被选中”这一事件,则M中的结果有3种:(
被选中”这一事件,则M中的结果有3种:(![]() ),(
),(![]() ,(
,(![]() ).
).
由于所有12种结果是等可能的,其中事件M中的结果有3种,因此,由古典概型的概率计算公式可得:
P(M)=![]()
(Ⅱ)用N表示“![]() 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件![]() 表示“
表示“![]() 全被选中”这一事件.由于
全被选中”这一事件.由于![]() 中只有(
中只有(![]() )一种结果.
)一种结果.
∴P(![]() )=
)=![]() 由对立事件的概率公式得:
由对立事件的概率公式得:
P(N)=1一P(![]() )=1一
)=1一![]() =
=![]()

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
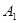 ,A
,A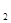 ,A
,A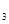 ,A
,A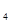 共4人;女干部有B
共4人;女干部有B ,B
,B