题目内容
10.已知α为第二象限角,且$\frac{1-tanα}{1+tanα}$=$\frac{4}{3}$,则tan($\frac{α}{2}$+$\frac{π}{8}$)=-3,sin(α+$\frac{π}{12}$)=$\frac{4-3\sqrt{3}}{10}$.分析 由条件利用同角三角函数的基本关系,求得sinα和cosα的值,再利用两角和差的三角公式求得sin(α+$\frac{π}{4}$)和cos(α+$\frac{π}{4}$)的值,利用半径公式求得 tan($\frac{α}{2}$+$\frac{π}{8}$)的值.再求的sin$\frac{π}{12}$ 和cos$\frac{π}{12}$的值,可得sin(α+$\frac{π}{12}$)的值.
解答 解:∵a为第二象限角,且$\frac{1-tanα}{1+tanα}$=$\frac{4}{3}$,∴tanα=-$\frac{1}{7}$=$\frac{sinα}{cosα}$,
又 sin2α+cos2α=1,∴sinα=$\frac{\sqrt{2}}{10}$,cosα=-$\frac{7\sqrt{2}}{10}$,
∴sin(α+$\frac{π}{4}$)=sinαcos$\frac{π}{4}$+cosαsin$\frac{π}{4}$=-$\frac{3}{5}$,
cos(α+$\frac{π}{4}$)=cosαcos$\frac{π}{4}$-sinαsin$\frac{π}{4}$=-$\frac{4}{5}$.
∴tan($\frac{α}{2}$+$\frac{π}{8}$)=$\frac{1-cos(α+\frac{π}{4})}{sin(α+\frac{π}{4})}$=$\frac{1+\frac{4}{5}}{-\frac{3}{5}}$=-3.
∵sin$\frac{π}{12}$=$\sqrt{\frac{1-cos\frac{π}{6}}{2}}$=$\frac{\sqrt{2-\sqrt{3}}}{2}$=$\frac{\sqrt{6}-\sqrt{2}}{4}$,cos$\frac{π}{12}$=$\sqrt{\frac{1+cos\frac{π}{6}}{2}}$=$\frac{\sqrt{2+\sqrt{3}}}{2}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
sin(α+$\frac{π}{12}$)=sinαcos$\frac{π}{12}$+cosαsin$\frac{π}{12}$=$\frac{\sqrt{2}}{10}$•$\frac{\sqrt{6}+\sqrt{2}}{4}$-$\frac{7\sqrt{2}}{10}$•$\frac{\sqrt{6}-\sqrt{2}}{4}$=$\frac{4-3\sqrt{3}}{10}$.
故答案为:-3;$\frac{4-3\sqrt{3}}{10}$.
点评 本题主要考查两角和差的三角公式,同角三角函数的基本关系,半角公式的应用,属于基础题.

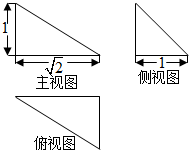
| A. | π | B. | 2π | C. | 3π | D. | 4π |
 如图,△BCD与△ECD都是边长为2的正三角形,平面ECD⊥平面BCD,AB⊥平面BCD,AB=2$\sqrt{3}$.
如图,△BCD与△ECD都是边长为2的正三角形,平面ECD⊥平面BCD,AB⊥平面BCD,AB=2$\sqrt{3}$.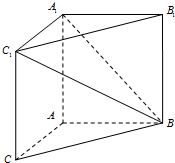 如图,在三棱柱ABC-A1B1C1中,AB=3,AA1=AC=4,AA1⊥平面ABC; AB⊥AC,
如图,在三棱柱ABC-A1B1C1中,AB=3,AA1=AC=4,AA1⊥平面ABC; AB⊥AC, 已知:椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,短半轴长为$\sqrt{3}$;斜率为$\frac{b}{a}$的动直线l与椭圆C交于A,B两点,与x轴,y轴相交于P,Q两点(如图所示).
已知:椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,短半轴长为$\sqrt{3}$;斜率为$\frac{b}{a}$的动直线l与椭圆C交于A,B两点,与x轴,y轴相交于P,Q两点(如图所示).