题目内容
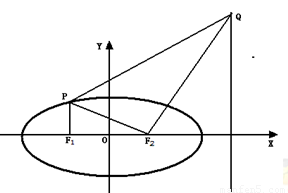
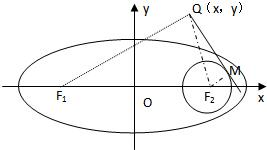
如图,点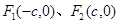 分别是椭圆C:
分别是椭圆C: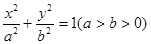 的左、右焦点,过点
的左、右焦点,过点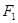 作
作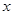 轴的垂线,交椭圆
轴的垂线,交椭圆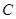 的上半部分于点
的上半部分于点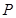 ,过点
,过点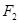 作
作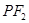 的垂线交直线
的垂线交直线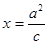 于点
于点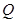 .
.
(1)如果点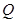 的坐标为(4,4),求椭圆
的坐标为(4,4),求椭圆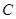 的方程;
的方程;
(2)试判断直线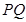 与椭圆
与椭圆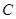 的公共点个数,并证明你的结论.
的公共点个数,并证明你的结论.
【答案】
(1)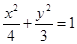 ;(2)1个.
;(2)1个.
【解析】
试题分析:(1)要求椭圆方程,由于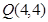 ,需要通过已知条件表示出
,需要通过已知条件表示出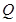 点的坐标,由于
点的坐标,由于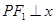 轴,则
轴,则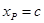 ,代入椭圆方程求得点
,代入椭圆方程求得点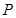 的纵坐标
的纵坐标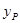 ,从而求得直线
,从而求得直线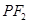 的斜率,根据
的斜率,根据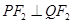 求的直线
求的直线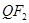 的斜率,有直线方程的点斜式求出直线
的斜率,有直线方程的点斜式求出直线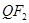 的方程,直线
的方程,直线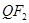 的方程与
的方程与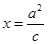 联立求得点
联立求得点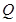 的坐标,从而求得
的坐标,从而求得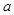 、
、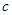 ,由于椭圆中
,由于椭圆中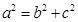 可求出
可求出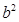 ,即可求得椭圆的方程;(2)要判断直线
,即可求得椭圆的方程;(2)要判断直线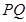 与椭圆
与椭圆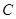 的公共点个数,需要求出直线
的公共点个数,需要求出直线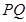 的方程,与椭圆方程联立,消去
的方程,与椭圆方程联立,消去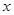 或
或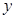 得到关于
得到关于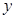 或
或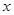 得一元二次方程,通过判断这个方程的的根的情况,即可得出所求的交点的个数.
得一元二次方程,通过判断这个方程的的根的情况,即可得出所求的交点的个数.
试题解析:解方程组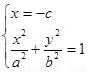 得
得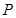 点的坐标为
点的坐标为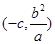 ,
,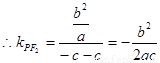 ,
,
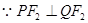 ,
,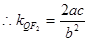 ,
,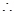 直线
直线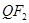 的方程为
的方程为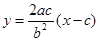 ,
,
将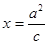 代入上式解得
代入上式解得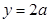 ,
,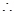
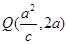 .
4分
.
4分
(1)因为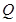 点的坐标为(4,4),所以
点的坐标为(4,4),所以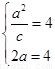 ,解得
,解得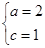 ,
,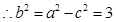 ,
,
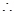 椭圆
椭圆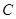 的方程为
的方程为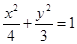 .
7分
.
7分
(2)
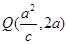 ,则
,则
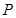 点的坐标为
点的坐标为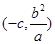 ,
,
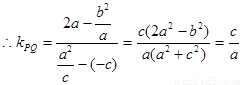 ,
,
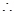
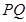 的方程为
的方程为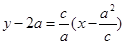 ,即
,即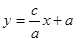 , 9分
, 9分
将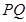 的方程代入椭圆
的方程代入椭圆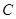 的方程得
的方程得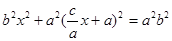 ,
,
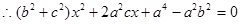 ①
①
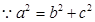 ,
,
方程①可化为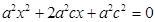 ,
,
解得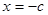 ,
,
所以直线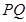 与椭圆
与椭圆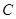 只有一个公共点
13分
只有一个公共点
13分
考点:椭圆的性质,直线与椭圆的位置关系.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 设F1,F2分别是椭圆C:
设F1,F2分别是椭圆C: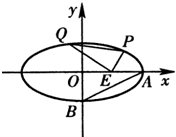 如图,已知中心在原点O、焦点在x轴上的椭圆C的离心率为
如图,已知中心在原点O、焦点在x轴上的椭圆C的离心率为 (2013•揭阳一模)如图,设点F1(-c,0)、F2(c,0)分别是椭圆
(2013•揭阳一模)如图,设点F1(-c,0)、F2(c,0)分别是椭圆 如图,已知F1,F2分别是椭圆C:
如图,已知F1,F2分别是椭圆C: