题目内容
设α,β,γ 都是锐角,且sinα+sinβ+sinγ=1,证明
(1)sin2α+sin2β+sin2γ≥
;
(2)tan2α+tan2β+tan2 γ≥
.
(1)sin2α+sin2β+sin2γ≥
| 1 |
| 3 |
(2)tan2α+tan2β+tan2 γ≥
| 3 |
| 8 |
证明:(1)由柯西不等式得:(sin2α+sin2β+sin2γ)(1+1+1)≥(1•sinα+1•sinβ+1•sinγ)2,
因为sinα+sinβ+sinγ=1,所以3(sin2α+sin2β+sin2γ)≥1,得:sin2α+sin2β+sin2γ≥
.
(2)由恒等式tan2x=
-1和若a,b,c>0,则
+
+
≥
,
得tan2α+tan2β+tan2 γ=
+
+
-3≥
-3.
于是
=
≥
=
,
由此得tan2α+tan2β+tan2 γ≥
-3=
.
因为sinα+sinβ+sinγ=1,所以3(sin2α+sin2β+sin2γ)≥1,得:sin2α+sin2β+sin2γ≥
| 1 |
| 3 |
(2)由恒等式tan2x=
| 1 |
| cos2x |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 9 |
| a+b+c |
得tan2α+tan2β+tan2 γ=
| 1 |
| cos2α |
| 1 |
| cos2β |
| 1 |
| cos2γ |
| 9 |
| cos2α+cos2β+cos2γ |
于是
| 9 |
| cos2α+cos2β+cos2γ |
| 9 |
| 3-(sin2α+sin2β+sin2γ) |
| 9 | ||
3-
|
| 27 |
| 8 |
由此得tan2α+tan2β+tan2 γ≥
| 27 |
| 8 |
| 3 |
| 8 |

练习册系列答案
相关题目
 (2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.
(2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.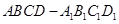 中,
中,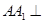 平面
平面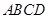 .
.
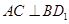 的充分条件,并给予证明;
的充分条件,并给予证明;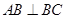 ,②
,②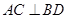 ;③
;③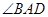 为锐角,求平面
为锐角,求平面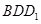 与平面
与平面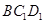 所成锐二面角
所成锐二面角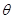 的取值范围.
的取值范围.