题目内容

设P为椭圆
x2
4
+
y2
3
=1上一动点，EF为圆N：（x-1）2+y2=1的任意一条直径，则
PE
•
PF
的取值范围是
[0，8]
[0，8]
．
分析：先把
PE
•
PF
转化为（
NE
-
NP
）•（
NF
-
NP
）=
NE
•
NF
-
NP
•（
NE
+
NF
）+
NP
2=-|NE|•|NF|•cosπ-0+|NP|2；再结合|NP|的范围即可求出结论．
解答：解：因为：
PE
•
PF
=（
NE
-
NP
）•（
NF
-
NP
）
=
NE
•
NF
-
NP
•（
NE
+
NF
）+
NP
2
=-|NE|•|NF|•cosπ-0+|NP|2
=-1+|NP|2．
又因为N为椭圆的右焦点
∴|NP|∈[a-c，a+c]=[1，3]
∴
PE
•
PF
∈[0，8]．
故答案为：[0，8]．
点评：本题主要考查椭圆的基本性质．解决本题的关键在于知道N为椭圆的右焦点并且会把所求问题转化．
练习册系列答案
相关题目
设圆C1：x2+y2-10x-6y+32=0，动圆C2：x2+y2-2ax-2（8-a）y+4a+12=0，
（Ⅰ）求证：圆C1、圆C2相交于两个定点；
（Ⅱ）设点P是椭圆
x24
+y2=1上的点，过点P作圆C1的一条切线，切点为T1，过点P作圆C2的一条切线，切点为T2，问：是否存在点P，使无穷多个圆C2，满足PT1=PT2？如果存在，求出所有这样的点P；如果不存在，说明理由．
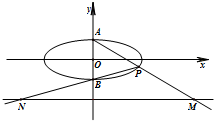在平面直角坐标系xOy中，如图，已知椭圆C：
x24
+y2=1的上、下顶点分别为A、B，点P在椭圆C上且异于点A、B，直线AP、BP与直线l：y=-2分别交于点M、N；
（I）设直线AP、BP的斜率分别为k1，k2求证：k1•k2为定值；
（Ⅱ）求线段MN长的最小值；
（Ⅲ）当点P运动时，以MN为直径的圆是否经过某定点？请证明你的结论．
（2012•江苏二模）如图，已知椭圆C：
x2
4
+y2=1，A、B是四条直线x=±2，y=±1所围成的两个顶点．
（1）设P是椭圆C上任意一点，若
OP
=m
OA
+n
OB
，求证：动点Q（m，n）在定圆上运动，并求出定圆的方程；
（2）若M、N是椭圆C上两个动点，且直线OM、ON的斜率之积等于直线OA、OB的斜率之积，试探求△OMN的面积是否为定值，说明理由．
如图，双曲线C1：
x2
4
-
y2
b2
=1与椭圆C2：
x2
4
+
y2
b2
=1（0＜b＜2）的左、右顶点分别为A1、A2第一象限内的点P在双曲线C1上，线段OP与椭圆C2交于点A，O为坐标原点．
（I）求证：
kAA1+kAA2
kPA1+kPA2
为定值（其中kAA1表示直线AA1的斜率，kAA2等意义类似）；
（II）证明：△OAA2与△OA2P不相似．
（III）设满足{（x，y）|
x2
4
-
y2
m2
=1，x∈R，y∈R}⊆{（x，y）|
x2
4
-
y2
3
＞1，x∈R，y∈R} 的正数m的最大值是b，求b的值．
（2011•重庆一模）已知抛物线y2=2px（p＞0）的焦点为椭圆
x2
4
+
y2
3
=1d的右焦点，点A、B为抛物线上的两点，O是抛物线的顶点，OA⊥OB．
（I）求抛物线的标准方程；
（Ⅱ）求证：直线AB过定点M（4，0）；
（III）设弦AB的中点为P，求点P到直线x-y=0的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网