题目内容
(2006
潍坊模拟)如下图,平面上两条直线AB与AP互相垂直,AB=1,AP=3,D在直线AB上,AD=4,平面上动点M在直线上的射影为N,满足DM=2BN(1)
求动点M的轨迹C的方程;(2)
若直线y=kx+m(k≠0,m≠0)与点M的轨迹C交于不同的两点E、F,且E、F都在以P为圆心的圆上,求实数m的取值范围.
答案:略
解析:
解析:
|
解析: (1)以A为原点,AB所在直线为x轴建立平面直角坐标系,则 B(1,0),D(4,0),P(0,3).设 M(x,y).则N(x,0),由  ,得 ,得 ,整理得点M的轨迹方程为 ,整理得点M的轨迹方程为
(2) 设 , ,
由 
消去 y整理得 , ,
依题意得
设 EF的中点为 , ,
则  , ,
∵点 G在直线y=kx+m上,∴  , ,
∴  , ,
∵ E、F两点都在以P(0,3)为圆心的同一圆上,∴ ,即 ,即 , ,
∴  ,整理得 ,整理得 , ,
代入 (*)式得
解得 m>0或 , ,
又  , ,
故所求 m的取值范围是 . . |

练习册系列答案
相关题目
(2006
潍坊模拟)下列函数中,图象经过平移或翻折后不能与函数 的图象重合的是
的图象重合的是
[
]|
A . |
B . |
|
C . |
D . |
(2006
潍坊模拟)如图所示,在杨辉三角中,斜线l的上方,从1开始按箭头所示的数组成一个锯齿形数列:1,3,3,4,6,5,10,…,记此数列为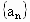 ,则
,则 等于
等于
[
]
|
A .55 |
B .65 |
C .66 |
D .78 |
(2006
潍坊模拟)已知a、b为常数, ,且a,
,且a, ,b成等比数列,
,b成等比数列, 的展开式中所有项的系数和为64,则a等于
的展开式中所有项的系数和为64,则a等于
[
]|
A . |
B . |
C .-1 |
D . |






