Question

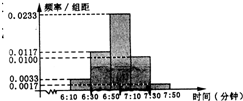（2012•莆田模拟）小明家订了一份《湄洲日报》，暑假期间他收集了每天报纸送达的时间的数据，并绘制成频率分布直方图如图所示．
（1）请你根据图中的数据信息，写出众数x₀=

7：00

（小时）；
（2）小明的父亲离家去上班的时间y在上午7：00～7：30之间，为此小明要求送报人每天在x₀时前后半小时内把报纸送达（每个时间点送达的可能性相等）
（i）求小明年的父亲在去上班前能取到报纸（称为事件A）的概率；
（ii）求小明的父亲一周5天（假日除外）能取到报纸的天数X的数学期望．

Answer 1

分析：（1）根据众数是频率分布直方图中最高矩形的底边中点的横坐标可得结论；
（2）（i）作出实验的所有的基本事件由平面区域，以及事件“小明的父亲能拿到报纸”（事件A）的基本事件，利用几何概型的概率公式解之即可；
（ii）分析可知小明的父亲一周5天（假日除外）能取到报纸的天数X服从二项分布，然后根据二项分布的数学期望公式解之即可．

解答：解：（1）观察频率分布直方图，频率最大在[6：50，7：10），众数x₀=7：00
故答案为：7：00
（2）记报纸送达的时间为x，x∈[6.5，7.5]
（i）如图所示，实验的所有的基本事件由平面区域Ω={（x，y）|6.5≤x≤7.5，7≤x≤7.5}
而事件“小明的父亲能拿到报纸”（事件A）的基本事件可由图中阴影部分表示
∵S_Ω=

1

2

×1=

1

2

，S_阴=

1

2

-

1

2

×

1

2

×

1

2

=

3

8

∴P（A）=

3

4

（ii） 依题意得，X～B（5，

3

4

）
∴EX=5×

3

4

=

15

4

故小明的父亲一周5天（假日除外）能取到报纸的天数X的数学期望为

15

4

点评：本题主要考查了众数的概念，以及频率分布直方图和离散型随机变量的概率分布，同时考查了识图能力和计算能力，属于基础题．