题目内容
(1)分解因式:x2-2xy+y2+2x-2y-3.(2)求sin30°-tan0°+ctg
| π |
| 4 |
| 5π |
| 6 |
(3)求函数y=
| lg(25-5x) |
| x+1 |
(4)已知直圆锥体的底面半径等于1cm,母线的长等于2cm,求它的体积.
(5)计算:10(2+
| 5 |
| 1 |
| 500 |
| 1 |
| 2 |
| 125 |
| 9 |
| 1 |
| 2 |
| ||
| 3 |
| 1 |
| 2 |
分析:(1) 把(x-y)看做一个整体,整式即:(x-y)2+2(x-y)-3
(2)应用特殊角的三角函数值.
(3)分母不为0,对数的真数大于0.
(4)先求出圆锥的高,代入体积公式计算.
(5)使用分数指数幂的运算法则化简每一项,然后合并同类项.
(2)应用特殊角的三角函数值.
(3)分母不为0,对数的真数大于0.
(4)先求出圆锥的高,代入体积公式计算.
(5)使用分数指数幂的运算法则化简每一项,然后合并同类项.
解答:解:(1)原式=(x-y)2+2(x-y)-3=(x-y-1)(x-y+3)
(2)原式=
-0+1-(-
)2=
(3)∵25-5x>0,且x+1≠0.∴x<2且x≠-1,∴所求定义域为:(-∞,-1)∪(-1,2).
(4)V=
π•12•
=
π(cm3)
(5)原式=10•(
-2 )-
+30•
=10
-20-10
+30
=-20+30•
=-20+
(
)
(2)原式=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 4 |
(3)∵25-5x>0,且x+1≠0.∴x<2且x≠-1,∴所求定义域为:(-∞,-1)∪(-1,2).
(4)V=
| 1 |
| 3 |
| 22-1 |
| ||
| 3 |
(5)原式=10•(
| 5 |
| 500 |
|
=10
| 5 |
| 5 |
|
=-20+30•
(
| ||||
(
|
10
| ||
| 3 |
| 5 |
| 7 |
| 2 |
点评:(1)体现整体的数学思想.
(2)记住特殊角的三角函数值.
(3)分式的分母不为0,对数的真数大于0.
(4)直接使用圆锥的体积公式.
(5)分数指数幂的运算法则的使用.本题的最后一项可能不对.
(2)记住特殊角的三角函数值.
(3)分式的分母不为0,对数的真数大于0.
(4)直接使用圆锥的体积公式.
(5)分数指数幂的运算法则的使用.本题的最后一项可能不对.

练习册系列答案
相关题目
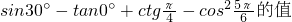 ,
,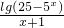 的定义域.
的定义域.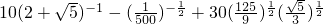 的值.
的值.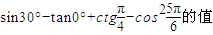 ,
,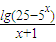 的定义域.
的定义域. 的值.
的值.