Question

如图，直三棱柱ABC-A₁B₁C₁中，AC=BC=AA₁，∠ACB=90°,E为AA₁的中点，D为AB的中点．

(Ⅰ)求异面直线CD与B₁E所成的角；

(Ⅱ)证明：B₁D⊥平面CDE；

(Ⅲ)求二面角C-B₁E-D的大小．

Answer 1

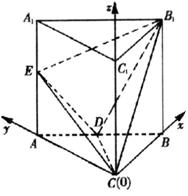
(法一)(Ⅰ)解：∵AC=BC，D是AB的中点，

∴CD⊥AB    又面A₁ABB₁⊥面ABC

∴CD⊥面A₁ABB₁    ∴CD⊥B₁E

∴异面直线CD与B₁E所成的角为90°

(Ⅱ)证：∵AB=AA₁   ∴

∴Rt△ADE∽Rt△BB₁D

∴∠ADE+∠BDB1=90°    ∴B₁D⊥DE

由(Ⅰ)知，B₁D⊥CD，  ∴B₁D⊥平面CDE

(Ⅲ)解：作DF⊥B₁E，垂足为F，连CF

根据三垂线定理，得CF⊥B₁E

∴∠CFD为二面角  C-B₁E-D的平面角

由平面几何知识，通过计算得DF=CD

∴∠CFD=45°，即二面角C-B₁E-D为45°的二面角

(法二)以CB、CA、CC₁为x轴、y轴、z轴建立空间直角坐标系O-xyz

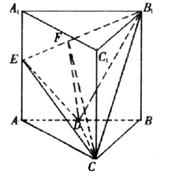
设CA=2，则C(0，0，0)，B(0，2，0)，A(2，0，0)，D(1，1，0)，B1(0，2，2)，E(2，0，1)

(Ⅰ) =(1，1，0)，=(2，-2，1)

∵·=0，  ∴⊥

则异面直线CD与B₁E所成的角为90°(4分)

(Ⅱ) =(1，-1，0)，=(1，1，0)，=(2，0，1)

∵·=·=0

∴⊥，⊥，即B₁D⊥CD，B₁D⊥CE

又CD∩CE=C，  ∴B₁D⊥平面CDE

(Ⅲ)由(1)、(Ⅱ)，CD⊥B₁E，CD⊥B₁D，有CD⊥平面B₁ED

则=(1，1，0)为面B₁ED的法向量

设n=(a，b，c)为面CB₁E的法向量，则

n⊥，n⊥，n·=n·=0，

而=(2，0，1)，=(0，2，2)

∴取a=1，此时n=(1，2，-2)

∵cos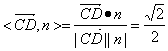

∴＜,n＞=45°

故二面角C-B₁E-D的大小为45°