题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,设m=(sinA,cosB),n=(cosA,sinB),
(Ⅰ)若m∥n,求角C;
(Ⅱ)若m⊥n,B=15°,a=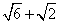 ,求边c。
,求边c。
(Ⅰ)若m∥n,求角C;
(Ⅱ)若m⊥n,B=15°,a=
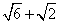 ,求边c。
,求边c。解:(Ⅰ)由m∥n sinAsinB-cosAcosB=0
sinAsinB-cosAcosB=0 cos(A+B)=0,
cos(A+B)=0,
因为0<A+B<180°,
所以A+B=90°,C=180°-(A+B)=90°.
(Ⅱ)由m⊥n sinAcosA+sinBcosB=0
sinAcosA+sinBcosB=0 sin2A+sin2B=0,
sin2A+sin2B=0,
已知B=15°,
所以sin2A+sin30°=0,sin2A= ,
,
因为0<2A<360°-2B=330°,
所以2A=210°,A=105°,C=180°-15°-105°=60°,
根据正弦定理 ,
,
因为 ,
,
所以 。
。
 sinAsinB-cosAcosB=0
sinAsinB-cosAcosB=0 cos(A+B)=0,
cos(A+B)=0,因为0<A+B<180°,
所以A+B=90°,C=180°-(A+B)=90°.
(Ⅱ)由m⊥n
 sinAcosA+sinBcosB=0
sinAcosA+sinBcosB=0 sin2A+sin2B=0,
sin2A+sin2B=0,已知B=15°,
所以sin2A+sin30°=0,sin2A=
 ,
,因为0<2A<360°-2B=330°,
所以2A=210°,A=105°,C=180°-15°-105°=60°,
根据正弦定理
 ,
,因为
 ,
,所以
 。
。
练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |