题目内容

已知函数f（x）=ax³+bx²+（b-a）x（a，b不同时为零的常数），导函数为f′（x）．
（1）当 $数学公式$ 时，若存在x∈[-3，-1]使得f′（x）＞0成立，求b的取值范围；
（2）求证：函数y=f′（x）在（-1，0）内至少有一个零点；
（3）若函数f（x）为奇函数，且在x=1处的切线垂直于直线x+2y-3=0，关于x的方程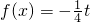 $数学公式$ 在[-1，t]（t＞-1）上有且只有一个实数根，求实数t的取值范围．

解：（1）当 $\text{[math]}$ 时，f′（x）= $\text{[math]}$ = $\text{[math]}$ ，
其对称轴为直线x=-b，当 $\text{[math]}$ ，解得 $\text{[math]}$ ，
当 $\text{[math]}$ ，b无解，
所以b的取值范围为 $\text{[math]}$ ；（4分）
（2）因为f′（x）=3ax²+2bx+（b-a），
∴f′（0）=b-a，f'（-1）=2a-b， $\text{[math]}$ ．
由于a，b不同时为零，所以 $\text{[math]}$ ，故结论成立．
（3）因为f（x）=ax³+bx²+（b-a）x为奇函数，所以b=0，所以f（x）=ax³-ax，
又f（x）在x=1处的切线垂直于直线x+2y-3=0．
所以a=1，即f（x）=x³-x．因为 $\text{[math]}$
所以f（x）在 $\text{[math]}$ 上是増函数，
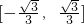在 $\text{[math]}$ 上是减函数，由f（x）=0解得x=±1，x=0，
如图所示，当 $\text{[math]}$ 时， $\text{[math]}$ ，即 $\text{[math]}$ ，解得 $\text{[math]}$ ；
当 $\text{[math]}$ 时， $\text{[math]}$ ，解得 $\text{[math]}$ ；当t=0时，显然不成立；
当 $\text{[math]}$ 时， $\text{[math]}$ ，即 $\text{[math]}$ ，解得 $\text{[math]}$ ；
当 $\text{[math]}$ 时， $\text{[math]}$ ，故 $\text{[math]}$ ．
所以所求t的取值范围是 $\text{[math]}$ 或 $\text{[math]}$ ．
分析：（1）当 $\text{[math]}$ 时，f′（x）= $\text{[math]}$ = $\text{[math]}$ ，由二次函数的性质，分类讨论可得答案；
（2）因为f′（x）=3ax²+2bx+（b-a），所以f′（0）=b-a，f'（-1）=2a-b， $\text{[math]}$ ．再由a，b不同时为零，所以 $\text{[math]}$ ，故结论成立；
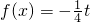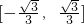（3）将“关于x的方程 $\text{[math]}$ 在[-1，t]（t＞-1）上有且只有一个实数根”转化为“函数f（x）与 $\text{[math]}$ 的交点”问题解决，先求函数f（x）因为f（x）=ax³+bx²+（b-a）x为奇函数，可解得b=0，所以f（x）=ax³-ax，再由“f（x）在x=1处的切线垂直于直线x+2y-3=0”解得a，从而得到f（x），再求导，由 $\text{[math]}$ ，知f（x $\text{[math]}$ 上是増函数，在 $\text{[math]}$ 上是减函数，明确函数的变化规律，再研究两个函数的相对位置求解．
点评：本题主要考查利用导数法研究函数的单调性，主要涉及了函数的奇偶性，函数的图象和性质以及方程的根转化为函数图象的交点解决等问题．