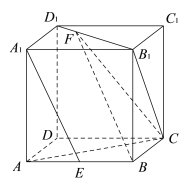
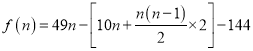题目内容
【题目】定义在R上的函数f（x）满足：f′（x）﹣f（x）=xex ， 且f（0）= 
，则 
的最大值为（ ）
A.0
B.
C.1
D.2
【答案】D
【解析】解：令F（x）= 
，则F′（x）= 
= 
=x，
则F（x）= 
x2+c，
∴f（x）=ex（ x2+c），
∵f（0）= ，
∴c= ，
∴f（x）=ex（ x2+ ），
∴f′（x）=ex（ x2+ ）+xex ，
∴ 
= 
，
设y= ，
则yx2+y=x2+2x+1，
∴（1﹣y）x2+2x+（1﹣y）=0，
当y=1时，x=0，
当y≠1时，要使方程有解，
则△=4﹣4（1﹣y）2≥0，
解得0≤y≤2，
故y的最大值为2，
故 的最大值为2，
故选：D．
先构造函数，F（x）= ，根据题意求出f（x）的解析式，即可得到 = ，再根据根的判别式即可求出最大值．
练习册系列答案
阅读快车系列答案
相关题目
