题目内容
(本小题满分14分)已知等比数列 的前
的前 项和为
项和为 ,
, ,
, ,且
,且 ,
, ,
, 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 满足
满足 ,求适合方程
,求适合方程 的正整数
的正整数 的值.
的值.
(1) ;(2)
;(2) .
.
【解析】
试题分析:本题主要考查等差中项、等比数列的通项公式、等比数列的前n项和公式、对数式的运算、裂项相消法等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,先利用等差中项的概念列出等式,再利用等比数列的通项公式将 转化成
转化成 和q,解出q的值,最后直接代入到
和q,解出q的值,最后直接代入到 中即可;第二问,先利用等比数列的前n项和将
中即可;第二问,先利用等比数列的前n项和将 展开,代入到
展开,代入到 ,利用对数式的运算,化简得到
,利用对数式的运算,化简得到 ,最后利用裂项相消法化简
,最后利用裂项相消法化简 ,然后解出n的值.
,然后解出n的值.
试题解析:(1)设数列 的公比为
的公比为 ,由
,由 ,得
,得 .
.
由 ,
, ,
, 成等差数列,
成等差数列,
故 ,所以
,所以 ,
,
得 ,故
,故 . 2分
. 2分
解得 ,或
,或 (舍). 4分
(舍). 4分
所以 ; 6分
; 6分
(2)由(1)得 ,
,
故 , 8分
, 8分
所以 . 9分
. 9分
 . 11分
. 11分

由题意得 .. 13分
.. 13分
解得 ,
,
 满足题意得
满足题意得 . 14分
. 14分
考点:等差中项、等比数列的通项公式、等比数列的前n项和公式、对数式的运算、裂项相消法.

练习册系列答案
相关题目
 ,则
,则 的最小值为________.
的最小值为________.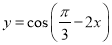 的图象向右平移
的图象向右平移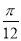 ,得到函数
,得到函数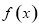 的图象,则函数
的图象,则函数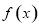 为( )
为( )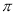 的奇函数 B.周期为
的奇函数 B.周期为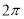 的奇函数 D.周期为
的奇函数 D.周期为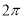 的偶函数
的偶函数 的图象向右平移
的图象向右平移 个单位后关于
个单位后关于 对称,当
对称,当 时,
时, <0恒成立,设
<0恒成立,设 ,
, ,
, ,则
,则 的大小关系为( )
的大小关系为( ) }定义如下:
}定义如下: =1,当
=1,当 时,
时, ,若
,若 ,则
,则 的值等于( )
的值等于( ) 是
是 ,则输出
,则输出 的值是 .
的值是 .
 (
( ,
, ,
, )的部分图象如图所示,则
)的部分图象如图所示,则 ( )
( )
 B.
B. C.
C. D.
D.
 恒成立,则实数
恒成立,则实数 的取值范围为 .
的取值范围为 . 是自然对数的底数,函数
是自然对数的底数,函数 的零点为
的零点为 ,函数
,函数 的零点为b,则下列不等式成立的是
的零点为b,则下列不等式成立的是


