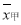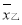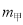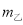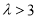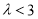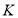题目内容
在数列{
}中，已知
（1）求
并由此猜想数列{}的通项公式
的表达式；
（2）用数学归纳法证明你的猜想。
（1）
=
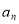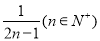； （2）见解析
【解析】
试题分析：（1）根据数列的递推公式不难求出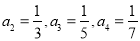
，由前四项的共同特征可归纳出通项公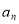式的表达式.
(2)根据数学归纳法的原理，证明分两步，第一，首先验证当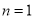
猜想正确；
第二，在假设
时猜想正确的前提下，证明当
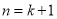时猜想也正确；由此可下结论对任何
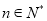,(1)中的猜想总是正确的.
试题解析：【解析】
（1）因为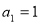
，
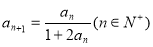
所以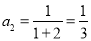
1分
2分
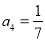3分
由此猜想数列{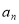
}的通项公式=
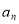4分
（2）下面用数学归纳法证明
①当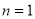
时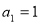，，猜想成立 5分
②假设当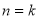
时，猜想成立，即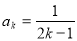
那么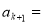
=
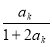10分
即当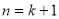
时，命题成立 11分
综合①②可知，猜想成立。 12分
考点：1、数列的递推公式；2、用数学归纳法证明与正整数有关的命题.
练习册系列答案
阅读快车系列答案
相关题目
