Question

已知数列{a_n}的通项公式an=n2+λn+2，若数列{a_n}为单调递增数列，则实数λ的取值范围是

[-2，+∞）

．

Answer 1

分析：方法一：利用函数单调性的定义，借助函数恒成立问题解决即可；
方法二：利用二次函数的性质，使其对称轴n=-

λ

2

＜

1+2

2

=

3

2

即可．

解答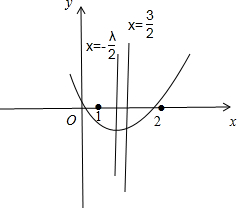：解解：方法一：
∵a_n=n²+λn+2，
∴a_n+1=（n+1）²+λ（n+1）+2，
∵数列{a_n}为单调递增数列，
∴a_n+1-a_n=2n+λ+1＞0（n∈N^*）恒成立，
∴λ＞-2n-1（n∈N^*）恒成立，
令f（n）=-2n-1（n∈N^*），
则λ＞f（x）_max=-2×1-1=-3
∴λ＞-3．
∴实数λ的取值范围是（-3，+∞）．
方法二：
∵a_n=n²+λn+2，
故a_n是n的二次函数，
又数列{a_n}为单调递增数列，
∴对称轴n=-

λ

2

＜

1+2

2

=

3

2

，如图：
∴λ＞-3．
故答案为：（-3，+∞）．

点评：本题考查数列的函数特性，考查函数单调性的定义应用，考查作图与识图能力，属于中档题．