题目内容
在xOy平面上有一点列P1(a1,b1),P2(a2,b2),…,Pn(an,bn),….对每一个正整数n,点Pn位于函数y=2 000·((1)求点Pn的纵坐标bn的表达式;
(2)若n∈N*,以bn、bn+1、bn+2为边长构成一个三角形,求a的取值范围.
解:(1)由点Pn、点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形知an=![]() =n+
=n+![]() ,∴bn=2 000·
,∴bn=2 000·![]() .
.
(2)∵函数y=2 000·(![]() )x(0<a<10)在R上是减函数,∴对n∈N*,有bn>bn+1>bn+2,则以bn、bn+1、bn+2为边长能构成一个三角形
)x(0<a<10)在R上是减函数,∴对n∈N*,有bn>bn+1>bn+2,则以bn、bn+1、bn+2为边长能构成一个三角形![]() bn+1+bn+2>bn,即(
bn+1+bn+2>bn,即(![]() )2+
)2+![]() -1>0.
-1>0.
解之得a<-5-5![]() 或a>-5+5
或a>-5+5![]() .
.
∴-5+5![]() <a<10.
<a<10.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
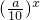 (0<a<10)的图象上,且点Pn(an,bn)与点(n,0)和(n+1,0)构成一个以点Pn(an,bn)为顶点的等腰三角形.
(0<a<10)的图象上,且点Pn(an,bn)与点(n,0)和(n+1,0)构成一个以点Pn(an,bn)为顶点的等腰三角形.