题目内容
已知函数f（x）=3sin（ωx+φ），g（x）=3cos（ωx+φ）若对任意x∈R，都有f（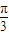
+x）=f（
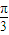-x），则g（
）= ．
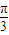【答案】分析：先根据f（
+x）=f（
-x）确定x=
是函数f（x）的对称轴，再由正余弦函数在其对称轴上取最值得到
ω+φ=
，（k∈Z），然后将x=
代入函数g（x）即可得到答案．
解答：解：由题意可知，f（
+x）=f（
-x），
∴x=
是函数f（x）的对称轴，且x=
时函数f（x）过最高点或最低点．
∴sin（
ω+φ）=±1，∴
ω+φ=
，（k∈Z）
g（
）=3cos（
ω+φ）=3cos（
）=0
故答案为：0
点评：本题主要考查三角函数的对称轴的问题．注意正余弦函数在其对称轴上取最值．
+x）=f（-x）确定x=是函数f（x）的对称轴，再由正余弦函数在其对称轴上取最值得到ω+φ=，（k∈Z），然后将x=代入函数g（x）即可得到答案．解答：解：由题意可知，f（
+x）=f（-x），∴x=
是函数f（x）的对称轴，且x=时函数f（x）过最高点或最低点．∴sin（
ω+φ）=±1，∴ω+φ=，（k∈Z）g（
）=3cos（ω+φ）=3cos（）=0故答案为：0
点评：本题主要考查三角函数的对称轴的问题．注意正余弦函数在其对称轴上取最值．
练习册系列答案
相关题目
已知函数f（x）=3•2x-1，则当x∈N时，数列{f（n+1）-f（n）}（ ）
| A、是等比数列 | B、是等差数列 | C、从第2项起是等比数列 | D、是常数列 |