题目内容
已知圆o: ![]() 与椭圆
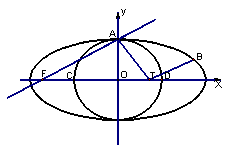
与椭圆![]() 有一个公共点A(0,1),F为椭圆的左焦点,直线AF被圆所截得的弦长为1.
有一个公共点A(0,1),F为椭圆的左焦点,直线AF被圆所截得的弦长为1.
(1)求椭圆方程。
(2)圆o与x轴的两个交点为C、D,B![]() 是椭圆上异于点A的一个动点,在线段CD上是否存在点T
是椭圆上异于点A的一个动点,在线段CD上是否存在点T![]() ,使
,使![]() ,若存在,请说明理由。
,若存在,请说明理由。
答案

⑵解法一:假设存在这样的点![]() ,使得
,使得![]() ,则点
,则点![]() 必定在线段
必定在线段![]() 的中垂线上……8分
的中垂线上……8分
设点![]() ,
,
①直线![]() 斜率存在时,设直线
斜率存在时,设直线![]()
由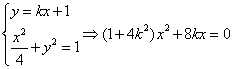 ,
,
![]() ,
,![]()
则![]() 的中点
的中点![]() ……………………7分
……………………7分
由![]() 可知
可知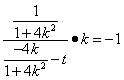 即
即![]()
∴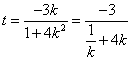
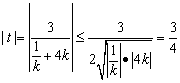 且
且![]() …………………9分
…………………9分
![]() 且
且![]()
 ⑵解法二:
⑵解法二:
设点B![]()
![]() ,由
,由![]() 知
知![]()
即![]() ,整理得
,整理得![]() ……………7分
……………7分
又∵![]() ,∴
,∴![]()
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
又∵![]() ,∴
,∴![]() ……………10分
……………10分
又圆O:![]()
综上可知在线段CD上存在点T,使得![]() ……………12分
……………12分

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
 已知圆o:x2+y2=b2与椭圆
已知圆o:x2+y2=b2与椭圆 ,直线
,直线 恒过定点F. 设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为
恒过定点F. 设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为 .
.  与椭圆C有4个相异公共点,试分别判断圆O与直线l1:mx+ny=1和l2:mx+ny=4的位置关系.
与椭圆C有4个相异公共点,试分别判断圆O与直线l1:mx+ny=1和l2:mx+ny=4的位置关系. ,直线
,直线 恒过定点F. 设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为
恒过定点F. 设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为 .
.
 与椭圆C有4个相异公共点,试分别判断圆O与直线l1:mx+ny=1和l2:mx+ny=4的位置关系.
与椭圆C有4个相异公共点,试分别判断圆O与直线l1:mx+ny=1和l2:mx+ny=4的位置关系.