题目内容
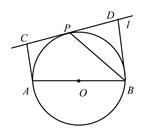
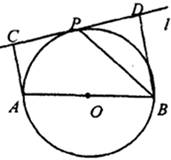
 22、如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:
22、如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:(1)l是⊙O的切线;
(2)PB平分∠ABD.
分析:(1)要证明l是⊙O的切线,可利用切线的判定定理,由于P点已经在圆上,故我们可以证明l与过P点的半径垂直,即可得到结论;
(2)要想得到PB平分∠ABD,即证∠DBP=∠ABP,观察到已知中及(1)的结论中有多个垂直关系,又由AB为直径也可得到∠APB=90°,故可以结合弦切角定理,利用等量代换的思想解决问题.
(2)要想得到PB平分∠ABD,即证∠DBP=∠ABP,观察到已知中及(1)的结论中有多个垂直关系,又由AB为直径也可得到∠APB=90°,故可以结合弦切角定理,利用等量代换的思想解决问题.
解答: 证明:(1)连接OP,
证明:(1)连接OP,
因为AC⊥l,BD⊥l,
所以AC∥BD.
又OA=OB,PC=PD,
所以OP∥BD,
从而OP⊥l.
因为P在⊙O上,
所以l是⊙O的切线.
(2)连接AP,
因为l是⊙O的切线,
所以∠BPD=∠BAP.
又∠BPD+∠PBD=90°,
∠BAP+∠PBA=90°,
所以∠PBA=∠PBD,
即PB平分∠ABD.
 证明:(1)连接OP,
证明:(1)连接OP,因为AC⊥l,BD⊥l,
所以AC∥BD.
又OA=OB,PC=PD,
所以OP∥BD,
从而OP⊥l.
因为P在⊙O上,
所以l是⊙O的切线.
(2)连接AP,
因为l是⊙O的切线,
所以∠BPD=∠BAP.
又∠BPD+∠PBD=90°,
∠BAP+∠PBA=90°,
所以∠PBA=∠PBD,
即PB平分∠ABD.
点评:本题(1)考查的知识点是切线的判定定理:过半径的一端与半径垂直的直线是圆的切线,他的证明思路有两种,一是先做垂直,再证明线段长等于半径;一是先做半径然后证明直线与半径垂直.而在(2)中根据已知条件分析转化的方向也是解题的主要思想.解决就是寻找解题的思路,由已知出发,找寻转化方向和从结论出发寻找转化方向要结合在一起使用.

练习册系列答案
 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
[选做题]
A.选修4—1:几何证明选讲
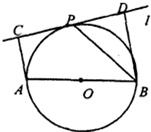
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:
(1)l是⊙O的切线;
(2)PB平分∠ABD.
|
二阶矩阵
 对应的变换将点
对应的变换将点 与
与 分别变换成点
分别变换成点 与
与 .求矩阵
.求矩阵 ;
;C.选修4—4:坐标系与参数方程
若两条曲线的极坐标方程分别为??=l与??=2cos(θ+),它们相交于A,B两点,求线
段AB的长.
D.选修4—5:不等式选讲
求函数
 的最大值.
的最大值. 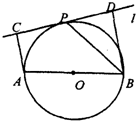 21、 选修1:几何证明选讲
21、 选修1:几何证明选讲