题目内容

已知函数数学公式，函数g（x）=x2-x+1，则函数h（x）=g（x）-f（x）有两个零点的a的范围是


  1. A.
    a≥1
  2. B.
    a≤1
  3. C.
    a≥0
  4. D.
    a≤0
D
分析：先令g（x）=f（x），分别画出函数f（x）与g（x）的简图，欲使函数h（x）=g（x）-f（x）有两个零点，由图可知，a要小于0．由此求得实数a的取值范围．
解答：解：令h（x）=g（x）-f（x）=0，
则g（x）=f（x），
分别画出函数f（x）与g（x）的简图如图，
当分段函数的分界点a小于0时，函数f（x）与g（x）的图象有两个交点．
即函数h（x）=g（x）-f（x）有两个零点．
故选D．
点评：本题主要考查函数的零点以及数形结合方法，数形结合是数学解题中常用的思想方法，能够变抽象思维为形象思维，有助于把握数学问题的本质；另外，由于使用了数形结合的方法，很多问题便迎刃而解，且解法简捷．
练习册系列答案
相关题目
已知函数f（x）=x2+ax-lnx，a∈R．
（Ⅰ）若a=0时，求曲线y=f（x）在点（1，f（1））处的切线方程；
（Ⅱ）若函数f（x）在[1，2]上是减函数，求实数a的取值范围；
（Ⅲ）令g（x）=f（x）-x2，是否存在实数a，当x∈（0，e]（e是自然常数）时，函数g（x）的最小值是3，若存在，求出a的值；若不存在，说明理由．
已知函数f（x）=x2+2（1-a）x+2（1-a）ln（x-1）x∈（1，+∞）．
（1）x=
3
2
是函数的一个极值点，求a的值；
（2）求函数f（x）的单调区间；
（3）当a=2时，函数g（x）=-x2-b，（b＞0），若对任意m1，m2∈[
1
e
+1，e+1]，
.
g(m2)-f(m1) 
  
.
＜2g2+2g都成立，求b的取值范围．
已知函数f（x）的图象在[a，b]上连续不断曲线，定义：f1（x）=min{f（t）|a≤t≤x}（x∈[a，b]），f2（x）=max{f（t）|a≤t≤x}（x∈[a，b]）．其中，min{f（t）|t∈D}表示函数f（t）在D上的最小值，max{f（t）|x∈D}表示函数f（t）在D上的最大值．若存在最小正整数k，使得f2（x）-f1（x）≤k（x-a）对任意的x∈[a，b]成立，则称函数f（x）为[a，b]上的“k阶收缩函数”．
（1）已知函数f（x）=2sinx（0≤x≤
n
2
），试写出f1（x），f2（x）的表达式，并判断f（x）是否为[0，
n
2
]上的“k阶收缩函数”，如果是，请求对应的k的值；如果不是，请说明理由；
（2）已知b＞0，函数g（x）=-x3+3x2是[0，b]上的2阶收缩函数，求b的取值范围．
已知函数f（x）=x2+2（1-a）x+2（1-a）ln（x-1）x∈（1，+∞）．
（1）x=
3
2
是函数的一个极值点，求a的值；
（2）求函数f（x）的单调区间；
（3）当a=2时，函数g（x）=-x2-b，（b＞0），若对任意m1，m2∈[
1
e
+1，e+1]，
.
g(m2)-f(m1) 
  
.
＜2g2+2g都成立，求b的取值范围．
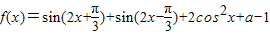已知函数（a为常数），若函数f（x）的最大值为．
（1）求实数a的值；
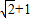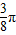（2）将函数y=f（x）的图象向左平移个单位，再向下平移2个单位得到函数y=g（x）的图象，求函数g（x）的单调递减区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网