题目内容
设二次函数f(x)＝ax2＋bx＋c(a＞b＞c)，已知f(1)＝0，且存在实数m，使f(m)＝－a．
(1)试推断f(x)在区间[0，＋∞)上是否为单调函数，并说明你的理由；
(2)设g(x)＝f(x)＋bx，对于x1，x2∈R，且x1≠x2，若g(x1)＝g(x2)＝0，求|x1－x2|的取值范围；
(3)求证：f(m＋3)＞0．
答案：
解析：
解析：
|
解(1) (2)据题意x1．x2是方程 (3) |
∴方程
有实根
(3分)
的两实根．
8分
14分
练习册系列答案
相关题目
R，且x＋y＋z＝1，求证x2＋y2＋z2≥
；
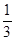，若x
． 