Question

已知关于t的一元二次方程

（1）当方程有实根时，求点的轨迹方程．

（2）求方程的实根的取值范围．

Answer 1

（1）设实根为t，则

即

根据复数相等的充要条件得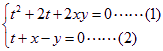

由（2）得代入（1）得

即……（3）

∴所求点的轨迹方程为，轨迹是以（1，－1）为圆心，为半径的圆．

（2）由（3）得圆心为（1，－1），半径，

直线与圆有公共点，则，

即    ∴，

故方程的实根的取值范围为．

解析:

（1）本题方程中有三个未知数由复数相等的充要条件能得到两个等式，而结论是要求动点的轨迹方程，联想到解析几何知识，求的轨迹方程就是求关于的方程，于是上面的两个等式正是轨迹方程的参数形式，消去参数t，问题得解

（2）由上面解答过程中的②知可看作一条直线，由③知是一个圆，因此求实根t的范围可转化为直线与圆有公共点的问题．