Question

在平面直角坐标系xOy中，已知椭圆（a＞b＞0）的离心率为，其焦点在圆x²+y²=1上．
（1）求椭圆的方程；
（2）设A，B，M是椭圆上的三点（异于椭圆顶点），且存在锐角θ，使．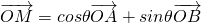
（i）求证：直线OA与OB的斜率之积为定值；
（ii）求OA²+OB²．

Answer 1

解：（1）依题意，得  c=1．于是，a=，b=1

所以所求椭圆的方程为

（2）（i）设A（x₁，y₁），B（x₂，y₂），
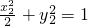则①，②．
又设M（x，y），因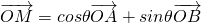，故

因M在椭圆上，故．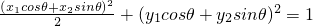
整理得．
将①②代入上式，并注意cosθsinθ≠0，得  ．
所以，为定值

（ii），故y₁²+y₂²=1．
又，故x₁²+x₂²=2．
所以，OA²+OB²=x₁²+y₁²+x₂²+y₂²=3

分析：（1）由已知中椭圆的离心率为，其焦点在圆x²+y²=1上我们可以求出a，b，c的值，进而得到椭圆的方程；
（2）（i）设A（x₁，y₁），B（x₂，y₂），M（x，y），由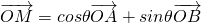．可得x，y的坐标表达式，进而根据M在椭圆上，可得为定值．
（ii）由（i）中结论，可得y₁²+y₂²=1，及x₁²+x₂²=2，进而得到OA²+OB²
点评：本题主要考查圆、椭圆及直线的基础知识，考查运算能力及探究能力．第（2）问中，可以证明线段AB的中点恒在定椭圆x²+2y²=1上．后一问与前一问之间具有等价关系．