题目内容
(本小题满分12分)
在等边![]() 中,
中,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 边上的点,满足
边上的点,满足![]()
![]() (如图1), 将
(如图1), 将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使二面角
的位置,使二面角![]() 成直二面角,连结
成直二面角,连结![]() 、
、![]() (如图2)
(如图2)
 (Ⅰ)求证:
(Ⅰ)求证:![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的大小。
所成角的大小。
解:不妨设正三角形![]() 的边长为3,则
的边长为3,则
(Ⅰ)在图1中,取![]() 中点
中点![]() ,连结
,连结![]() ,
,
则∵ ![]() ,
,
 ∴
∴![]() 而
而![]() ,
,
即 △![]() 是正三角形
是正三角形
又∵![]() , ∴
, ∴![]()
∴在图2中有![]() ,
,![]() ,
,
∴![]() 为二面角
为二面角![]() 的平面角
的平面角
∵二面角![]() 为直二面角, ∴
为直二面角, ∴![]()
又∵![]() , ∴
, ∴![]() ⊥平面
⊥平面![]() ,即
,即![]() ⊥平面
⊥平面![]() .
.
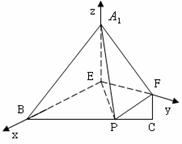
(Ⅱ)由(Ⅰ)可知![]() ⊥平面
⊥平面![]() ,
,![]() ,建立如图的坐标系,则
,建立如图的坐标系,则
![]() .
.
在图1中,不难得到EF∥DP![]() ,且
,且![]() ;DE∥FP,
;DE∥FP,![]()
故点P的坐标![]() ,
,
∴![]() ,
,![]() ,
,![]()
不妨设平面![]() 的法向量
的法向量![]() ,则
,则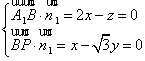
令![]() 得
得![]() ∴
∴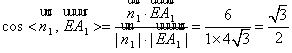
∵![]()
故直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.

练习册系列答案
相关题目