题目内容
定义F(x,y)=yx(x>0,y>0).
(1)设函数f(n)=
(n∈N*),求函数f(n)的最小值;
(2)设g(x)=F(x,2),正项数列{an}满足;a1=3,g(an+1)=8an,求数列{an}的通项公式,并求所有可能乘积aiaj(1≤i≤j≤n)的和.
(1)设函数f(n)=
| F(n,2) | F(2,n) |
(2)设g(x)=F(x,2),正项数列{an}满足;a1=3,g(an+1)=8an,求数列{an}的通项公式,并求所有可能乘积aiaj(1≤i≤j≤n)的和.
分析:(1)由题意可得f(n)=
=
,要求f(n)的最小值,只要判断f(n)的单调性,利用比较法中的比商:
=
,只要判断2n2与(n+1)2的大小即可判断
(2)先由 条件可求g(x)=F(x,2)=2x,代入可得g(an+1)=2an+1,结合g(an+1)=8an=23an,可得an+1与an的递推关系,进而可求通项,设所求的和为S,则S=a1•a1+(a1+a2)•a2+…+(a1+a2+…+an)•an利用分组求和的可求
| F(n,2) |
| F(2,n) |
| 2n |
| n2 |
| f(n+1) |
| f(n) |
| 2n2 |
| (n+1)2 |
(2)先由 条件可求g(x)=F(x,2)=2x,代入可得g(an+1)=2an+1,结合g(an+1)=8an=23an,可得an+1与an的递推关系,进而可求通项,设所求的和为S,则S=a1•a1+(a1+a2)•a2+…+(a1+a2+…+an)•an利用分组求和的可求
解答:解:(1)∵F(x,y)=yx(x>0,y>0).
∴f(n)=
=
,
∴
=
•
=
,
由于2n2-(n+1)2=(n-1)2-2,
当n≥3时,f(n+1)>f(n); 当n<3时,f(n+1)<f(n),
所以当n=3时,f(n)min=f(3)=
;…(6分)
(2)∵g(x)=F(x,2)=2x,
∴g(an+1)=2an+1,
又∵g(an+1)=8an=23an,
所以an+1=3an,而a1=3,所以an=3n;…(9分)
设所求的和为S,
则S=a1•a1+(a1+a2)•a2+…+(a1+a2+…+an)•an…(11分)
=3•31+(3+32)•32+…+(3+32+…+3n)•3n…(12分)
=
•31+
•32+…+
•3n
=-
(3+32+…+3n)+
(9+92+…+9n)
=-
•
+
•
=
×9n+1-
×3n+2+
…(14分).
∴f(n)=
| F(n,2) |
| F(2,n) |
| 2n |
| n2 |
∴
| f(n+1) |
| f(n) |
| 2n+1 |
| (n+1)2 |
| n2 |
| 2n |
| 2n2 |
| (n+1)2 |
由于2n2-(n+1)2=(n-1)2-2,
当n≥3时,f(n+1)>f(n); 当n<3时,f(n+1)<f(n),
所以当n=3时,f(n)min=f(3)=
| 8 |
| 9 |
(2)∵g(x)=F(x,2)=2x,
∴g(an+1)=2an+1,
又∵g(an+1)=8an=23an,
所以an+1=3an,而a1=3,所以an=3n;…(9分)
设所求的和为S,
则S=a1•a1+(a1+a2)•a2+…+(a1+a2+…+an)•an…(11分)
=3•31+(3+32)•32+…+(3+32+…+3n)•3n…(12分)
=
| 3(1-31) |
| 1-3 |
| 3(1-32) |
| 1-3 |
| 3(1-31) |
| 1-3 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
=-
| 3 |
| 2 |
| 3(1-3n) |
| 1-3 |
| 3 |
| 2 |
| 9(1-9n) |
| 1-9 |
=
| 3 |
| 16 |
| 1 |
| 4 |
| 9 |
| 16 |
点评:本题主要考查了利用单调性求解函数的最值,及分组求和方法、等比数列的通项公式的应用,属于函数与数列知识的综合应用.

练习册系列答案
相关题目
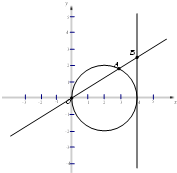 (2011•南汇区二模)已知动直线y=kx交圆(x-2)2+y2=4于坐标原点O和点A,交直线x=4于点B,若动点M满足
(2011•南汇区二模)已知动直线y=kx交圆(x-2)2+y2=4于坐标原点O和点A,交直线x=4于点B,若动点M满足